Rank 3 permutation group
In mathematical finite group theory, a rank 3 permutation group acts transitively on a set such that the stabilizer of a point has 3 orbits. The study of these groups was started by Higman (1964, 1971). Several of the sporadic simple groups were discovered as rank 3 permutation groups.
Classification
The primitive rank 3 permutation groups are all in one of the following classes:
- Cameron (1981) classified the ones such that
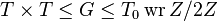where the socle T of T0 is simple, and T0 is a 2-transitive group of degree √n. - Liebeck (1987) classified the ones with a regular elementary abelian normal subgroup
- Bannai (1971–72) classified the ones whose socle is a simple alternating group
- Kantor & Liebler (1982) classified the ones whose socle is a simple classical group
- Liebeck & Saxl (1986) classified the ones whose socle is a simple exceptional or sporadic group.
Examples
If G is any 4-transitive group acting on a set S, then its action on pairs of elements of S is a rank 3 permutation group.[1] In particular most of the alternating groups, symmetric groups, and Mathieu groups have 4-transitive actions, and so can be made into rank 3 permutation groups.
The projective general linear group acting on lines in a projective space of dimension at least 3 is a rank-3 permutation group.
Several 3-transposition groups are rank-3 permutation groups (in the action on transpositions).
It is common for the point-stabilizer of a rank-3 permutation group acting on one of the orbits to be a rank-3 permutation group. This gives several "chains" of rank-3 permutation groups, such as the Suzuki chain and the chain ending with the Fischer groups.
Some unusual rank-3 permutation groups (many from (Liebeck & Saxl 1986)) are listed below.
| Group | Point stabilizer | size | Comments |
|---|---|---|---|
| A6 = L2(9) = Sp4(2)' = M10' | S4 | 15 = 1+6+8 | Pairs of points, or sets of 3 blocks of 2, in the 6-point permutation representation; two classes |
| A9 | L2(8):3 | 120 = 1+56+63 | Projective line P1(8); two classes |
| A10 | (A5×A5):4 | 126 = 1+25+100 | Sets of 2 blocks of 5 in the natural 10-point permutation representation |
| L2(8) | 7:2 = Dih(7) | 36 = 1+14+21 | Pairs of points in P1(8) |
| L3(4) | A6 | 56 = 1+10+45 | Hyperovals in P2(4); three classes |
| L4(3) | PSp4(3):2 | 117 = 1+36+80 | Symplectic polarities of P3(3); two classes |
| G2(2)' = U3(3) | PSL3(2) | 36 = 1+14+21 | Suzuki chain |
| U3(5) | A7 | 50 = 1+7+42 | The action on the vertices of the Hoffman-Singleton graph; three classes |
| U4(3) | L3(4) | 162 = 1+56+105 | Two classes |
| Sp6(2) | G2(2) = U3(3):2 | 120 = 1+56+63 | The Chevalley group of type G2 acting on the octonion algebra over GF(2) |
| Ω7(3) | G2(3) | 1080 = 1+351+728 | The Chevalley group of type G2 acting on the imaginary octonions of the octonion algebra over GF(3); two classes |
| U6(2) | U4(3):22 | 1408 = 1+567+840 | The point stabilizer is the image of the linear representation resulting from "bringing down" the complex representation of Mitchell's group (a complex reflection group) modulo 2; three classes |
| M11 | M9:2 = 32:SD16 | 55 = 1+18+36 | Pairs of points in the 11-point permutation representation |
| M12 | M10:2 = A6.22 = PΓL(2,9) | 66 = 1+20+45 | Pairs of points, or pairs of complementary blocks of S(5,6,12), in the 12-point permutation representation; two classes |
| M22 | 24:A6 | 77 = 1+16+60 | Blocks of S(3,6,22) |
| J2 | U3(3) | 100 = 1+36+63 | Suzuki chain; the action on the vertices of the Hall-Janko graph |
| Higman-Sims group HS | M22 | 100 = 1+22+77 | The action on the vertices of the Higman-Sims graph |
| M22 | A7 | 176 = 1+70+105 | Two classes |
| M23 | M21:2 = L3(4):22 = PΣL(3,4) | 253 = 1+42+210 | Pairs of points in the 23-point permutation representation |
| M23 | 24:A7 | 253 = 1+112+140 | Blocks of S(4,7,23) |
| McLaughlin group McL | U4(3) | 275 = 1+112+162 | The action on the vertices of the McLaughlin graph |
| M24 | M22:2 | 276 = 1+44+231 | Pairs of points in the 24-point permutation representation |
| G2(3) | U3(3):2 | 351 = 1+126+244 | Two classes |
| G2(4) | J2 | 416 = 1+100+315 | Suzuki chain |
| M24 | M12:2 | 1288 = 1+495+792 | Pairs of complementary dodecads in the 24-point permutation representation |
| Suzuki group Suz | G2(4) | 1782 = 1+416+1365 | Suzuki chain |
| G2(4) | U3(4):2 | 2016 = 1+975+1040 | |
| Co2 | PSU6(2):2 | 2300 = 1+1891+1408 | |
| Rudvalis group Ru | ²F₄(2) | 4060 = 1+1755+2304 | |
| Fi22 | 2.PSU6(2) | 3510 = 1+693+2816 | 3-transpositions |
| Fi22 | Ω7(3) | 14080 = 1+3159+10920 | Two classes |
| Fi23 | 2.Fi22 | 31671 = 1+3510+28160 | 3-transpositions |
| G2(8).3 | SU3(8).6 | 130816 = 1+32319+98496 | |
| Fi23 | PΩ8+(3).S3 | 137632 = 1+28431+109200 | |
| Fi24' | Fi23 | 306936 = 1+31671+275264 | 3-transpositions |
Notes
- ↑ The three orbits are: the fixed pair itself; those pairs having one element in common with the fixed pair; and those pairs having no element in common with the fixed pair.
References
- Bannai, Eiichi (1971–72), "Maximal subgroups of low rank of finite symmetric and alternating groups", Journal of the Faculty of Science. University of Tokyo. Section IA. Mathematics 18: 475–486, ISSN 0040-8980, MR 0357559
- Brouwer, A. E.; Cohen, A. M.; Neumaier, Arnold (1989), Distance-regular graphs, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)] 18, Berlin, New York: Springer-Verlag, ISBN 978-3-540-50619-5, MR 1002568
- Cameron, Peter J. (1981), "Finite permutation groups and finite simple groups", The Bulletin of the London Mathematical Society 13 (1): 1–22, doi:10.1112/blms/13.1.1, ISSN 0024-6093, MR 599634
- Higman, Donald G. (1964), "Finite permutation groups of rank 3", Mathematische Zeitschrift 86: 145–156, doi:10.1007/BF01111335, ISSN 0025-5874, MR 0186724
- Higman, Donald G. (1971), "A survey of some questions and results about rank 3 permutation groups", Actes du Congrès International des Mathématiciens (Nice, 1970) 1, Gauthier-Villars, pp. 361–365, MR 0427435
- Kantor, William M.; Liebler, Robert A. (1982), "The rank 3 permutation representations of the finite classical groups", Transactions of the American Mathematical Society 271 (1): 1–71, doi:10.2307/1998750, ISSN 0002-9947, MR 648077
- Liebeck, Martin W. (1987), "The affine permutation groups of rank three", Proceedings of the London Mathematical Society. Third Series 54 (3): 477–516, doi:10.1112/plms/s3-54.3.477, ISSN 0024-6115, MR 879395
- Liebeck, Martin W.; Saxl, Jan (1986), "The finite primitive permutation groups of rank three", The Bulletin of the London Mathematical Society 18 (2): 165–172, doi:10.1112/blms/18.2.165, ISSN 0024-6093, MR 818821