Range voting

| Part of the Politics series |
| Voting systems |
|---|
|
Multiple-winner |
|
|
Random selection |
|
| Politics portal |
Range voting is a voting method for single-seat elections, in which voters give each candidate a score, the scores are added or averaged, and the candidate with the highest total is elected. It has been described by various other names including the point system, ratings summation, 0-99 voting, average voting; cardinal, score and utility voting.
A form of range voting[1][2] was apparently used in some elections in Ancient Sparta by measuring how loudly the crowd shouted for different candidates;[3] rough modern-day equivalents include the use of clapometers in some television shows and the judging processes of some athletic competitions. Approval voting can be considered to be range voting with only two levels: approved (1) and disapproved (0).
Voting system
Range voting uses a ratings ballot; that is, each voter rates each candidate with a number within a specified range, such as 0 to 99 or 1 to 5. All candidates should be rated, unlike cumulative voting where voters are not permitted to provide scores for more than some number of candidates. The scores for each candidate are summed, and the candidate with the highest sum is the winner. If voters are explicitly allowed to abstain from rating certain candidates, as opposed to implicitly giving the lowest number of points to unrated candidates, then a candidate's score would be the average rating from voters who did rate this candidate.
In some competitions subject to judges' scores, a truncated mean is used to remove extreme scores. For example, range voting with truncated means is used in figure skating competitions to avoid the results of the third skater affecting the relative positions of two skaters who have already finished their performances (the independence of irrelevant alternatives), using truncation to mitigate biases of some judges who have ulterior motives to score some competitors too high or low.
Another method of counting ratings ballots is to find the median score of each candidate, and elect the candidate with the highest median score. This method is also referred to as Majority Judgment.[4][5] It could have the effect of reducing the incentive to exaggerate. A potential disadvantage is that multiway exact ties for winner may become common, although a method exists in Majority Judgment to break such ties.[4] In conventional range voting, these ties would be extremely rare. Another consequence of using medians is that adding an "all-zero ballot" can alter the election winner, which is arguably a disadvantage.
Range voting in which only two different votes may be submitted (0 and 1, for example) is equivalent to approval voting. As with approval voting, range voters must weigh the adverse impact on their favorite candidate of ranking other candidates highly.
Alternative use
The range voting concept has been used in non-political contexts also. Sports such as gymnastics rate competitors on a numeric scale, although the fact that judges' ratings are public makes it less likely for them to engage in blatant tactical voting. Range voting is common for things where there is no single winner: for instance on the Web, sites allow users to rate items such as movies (Internet Movie Database), comments, recipes, and many other things.
Dotmocracy is an established paper-based group facilitation method that invites participants to brainstorm ideas and then vote on a range of agreement for each idea in order to recognize which ideas have the most collective agreement.
Range voting has been used informally by various amateur clubs to make decisions such as meeting dates, event themes or what books to read.
Example
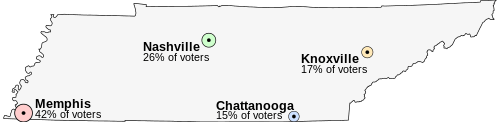
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.
The candidates for the capital are:
- Memphis, the state's largest city, with 42% of the voters, but located far from the other cities
- Nashville, with 26% of the voters, near the center of the state
- Knoxville, with 17% of the voters
- Chattanooga, with 15% of the voters
The preferences of the voters would be divided like this:
| 42% of voters (close to Memphis) |
26% of voters (close to Nashville) |
15% of voters (close to Chattanooga) |
17% of voters (close to Knoxville) |
|---|---|---|---|
|
|
|
|
Suppose that voters each decided to grant from 0 to 10 points to each city such that their most liked choice got 10 points, and least liked choice got 0 points, with the intermediate choices getting an amount proportional to their relative distance.
| Voter from/ City Choice |
Memphis | Nashville | Chattanooga | Knoxville | Total |
|---|---|---|---|---|---|
| Memphis | 420 (42 × 10) | 0 (26 × 0) | 0 (15 × 0) | 0 (17 × 0) | 420 |
| Nashville | 168 (42 × 4) | 260 (26 × 10) | 90 (15 × 6) | 85 (17 × 5) | 603 |
| Chattanooga | 84 (42 × 2) | 104 (26 × 4) | 150 (15 × 10) | 119 (17 × 7) | 457 |
| Knoxville | 0 (42 × 0) | 52 (26 × 2) | 90 (15 × 6) | 170 (17 × 10) | 312 |
Nashville, the capital in real life, likewise wins in the example. However, if voters from Knoxville and Chattanooga were to rate Nashville as 0 and/or both sets of voters were to rate Chattanooga as 10, the winner would be Chattanooga over Nashville by 508 to 428. This would be a better outcome for the voters in those cities than what they would get if they were to reflect their true preferences, and is considered to be an instance of tactical voting. Such tactical voting would be less effective if the ballots were counted using median scores.
For comparison, note that traditional first-past-the-post would elect Memphis, even though most citizens consider it the worst choice, because 42% is larger than any other single city. Instant-runoff voting would elect the 2nd-worst choice (Knoxville), because the central candidates would be eliminated early. A Two-round system would have a runoff between Memphis and Nashville where Nashville would win.
Properties
Range voting allows voters to express preferences of varying strengths.
Range voting satisfies the monotonicity criterion, i.e. raising your vote's score for a candidate can never hurt their chances of winning, and lowering it can never help their chances. Also, range voting satisfies the participation criterion, i.e. casting a sincere vote can never result in a worse election winner (from your point of view) than if you had simply abstained from voting.
Range voting is independent of clones in the sense that if there is a set of candidates such that every voter gives the same rating to every candidate in this set, then the probability that the winner is in this set is independent of how many candidates are in the set.
In summary, range voting satisfies the monotonicity criterion, the participation criterion, the consistency criterion, independence of irrelevant alternatives, resolvability criterion, and reversal symmetry. It is immune to cloning, except for the obvious specific case in which a candidate with clones ties, instead of achieving a unique win. It does not satisfy either the Condorcet criterion (i.e. is not a Condorcet method) or the Condorcet loser criterion, although with all-strategic voters and perfect information the Condorcet winner is a Nash equilibrium.[6] It does not satisfy the majority criterion, but it satisfies a weakened form of it: a majority can force their choice to win, although they might not exercise that capability. It does not satisfy the later-no-harm criterion, meaning that giving a positive rating to a less preferred candidate can cause a more preferred candidate to lose.
As it satisfies the criteria of a deterministic voting system, with non-imposition, non-dictatorship, monotonicity, and independence of irrelevant alternatives, it may appear that it violates Arrow's impossibility theorem. The reason that range voting is not regarded as a counter-example to Arrow's theorem is that it is a cardinal voting system, while the "universality" criterion of Arrow's theorem effectively restricts that result to ordinal voting systems.[7]
Strategy
In most cases, ideal range voting strategy for well-informed voters is identical to ideal approval voting strategy, and a voter would want to give his least and most favorite candidates a minimum and a maximum score, respectively. If one candidate's backers engaged in this tactic and other candidates' backers cast sincere rankings for the full range of candidates, then the tactical voters would have a significant advantage over the rest of the electorate. When the population is large and there are two obvious and distinct front-runners, tactical voters seeking to maximize their influence on the result would give a maximum rating to their preferred candidate, and a minimum rating to the other front-runner; these voters would then give minimum and maximum scores to all other candidates so as to maximize expected utility.
However, there are examples in which voting maximum and minimum scores for all candidates is not optimal.[8] Exit poll experiments have shown that voters tend to vote more sincerely for candidates they perceive have no chance of winning.[9] Thus range voting may yield higher support for third party and independent candidates, unless those candidates become viable, than other common voting methods, creating what has been called the "nursery effect".[10]
Range voting advocates argue that range voting systems (including approval voting) give no reason to ever dishonestly rank a less-preferred candidate over a more-preferred one in 3-candidate elections.[11] However, detractors respond that it provides motivation to rank a less-preferred and more-preferred candidate equally or near-equally (i.e., both 0-1 or both 98-99). This could lead to undemocratic results if different segments of the population used strategy at significantly different rates. (Note that traditional first-past-the-post voting forces all candidates except one to be ranked equally, so that all voters are compressing their preferences equally.)
Advocacy
Range voting is advocated online by the election reform sites RangeVote.com, The Center for Election Science, and the Center for Range Voting. Guy Ottewell, who helped develop the system of approval voting, now endorses range voting.[12] No elected official in the United States is known to endorse range voting.
See also
- List of democracy and elections-related topics
- Consensus decision-making
- Decision making
- Democracy
- Relative Utilitarianism
- Hot or Not — a real world example
Notes
- ↑ James S. Fishkin: The Voice of the People: Public Opinion & Democracy, Yale University Press 1995
- ↑ "Ancient Sparta used range voting... sort of".
- ↑ Stille, Alexander (2001-06-02). "Adding Up the Costs of Cyberdemocracy". New York Times. Retrieved 10/03/2009. Check date values in:
|accessdate=(help) - ↑ 4.0 4.1 Michel Balinski and Rida Laraki. "A theory of measuring, electing, and ranking — PNAS". Pnas.org. Retrieved 2009-08-03.
- ↑ "VotingMJL.dvi" (PDF). Retrieved 2009-08-03.
- ↑ Laslier, J.-F. (2006) "Strategic approval voting in a large electorate," IDEP Working Papers No. 405 (Marseille, France: Institut D'Economie Publique)
- ↑ Arrow, Kenneth (August 1950). "A Difficulty in the Concept of Social Welfare". The Journal of Political Economy 58 (4): 328–346. doi:10.1086/256963.
- ↑ "Examples in which best Range Voting strategy is not "approval style" voting". The center for range voting.
- ↑ "Honesty and Strategy in real-world voters". The center for range voting.
- ↑ "The "Nursery Effect" (Executive summary)". The center for range voting.
- ↑ "Completion of Gibbard-Satterthwaite impossibility theorem; range voting and voter honesty" (PDF). Warren Smith, Temple University.
- ↑ Ottewell, Guy (April 2004). "The Arithmetic of Voting". Universal Workbench. self published. Retrieved January 8, 2010.
External links
- The Center for Range Voting and its simplified introductory homepage
- The Center for Election Science includes an article on Range Voting
- RangeVote includes a user-friendly presentation on range voting
- Voting In Sanity includes a comprehensive description of the benefits of score voting
- Range voting discussion list at Yahoo Groups
- Discussion list on Google Groups
- FairVote criticism of approval, range voting, and Condorcet methods
- Mock 2008 U.S. Presidential Election using range voting
- Vote! web application that implements Range Voting, you can create your own ballots or vote in a few sample polls.
- Simulation of various voting models for close elections Article by Brian Olson.
- Mechanic, Michael; William Poundstone (2007-01-02). "The verdict is in: our voting system is a loser". Mother Jones (The Foundation for National Progress). Retrieved 2008-02-04.