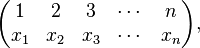Random permutation

A random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation. A good example of a random permutation is the shuffling of a deck of cards: this is ideally a random permutation of the 52 cards.

Generating random permutations

Entry-by-entry brute force method

One method of generating a random permutation of a set of length n uniformly at random (i.e., each of the n! permutations is equally likely to appear) is to generate a sequence by taking a random number between 1 and n sequentially, ensuring that there is no repetition, and interpreting this sequence (x1, ..., xn) as the permutation

\begin{pmatrix} 1 & 2 & 3 & \cdots & n \\ x_1 & x_2 & x_3 & \cdots & x_n \\ \end{pmatrix},

shown here in two-line notation.

This brute-force method will require occasional retries whenever the random number picked is a repeat of a number already selected. This can be avoided if, on the ith step (when x1, ..., xi − 1 have already been chosen), one chooses a number j at random between 1 and n − i + 1 and sets xi equal to the jth largest of the unchosen numbers.

Knuth shuffles

A simple algorithm to generate a permutation of n items uniformly at random without retries, known as the Knuth shuffle, is to start with any permutation (for example, the identity permutation), and then go through the positions 1 through n − 1, and for each position i swap the element currently there with a randomly chosen element from positions i through n, inclusive. It's easy to verify that any permutation of n elements will be produced by this algorithm with probability exactly 1/n!, thus yielding a uniform distribution over all such permutations.

The initialization to the identity permutation and the shuffling may be combined, as in the following example. It requires a function uniform(m) which returns a random integer between 0 and m inclusive.

unsigned uniform(unsigned i,unsigned m); /* Returns a random integer i <= uniform(i,m) <= m */
 
void permute(unsigned permutation[], unsigned n)
{
    unsigned i;
    for (i = 0; i < n; i++) {
        unsigned j = uniform(i, n - 1);
        unsigned swap = permutation[i];
        permutation[i] = permutation[j];
        permutation[j] = swap;
    }
}

Note that the first assignment to permutation[i] might be copying an uninitialized value, if j happens to be equal to i. However, in this case, it is immediately overwritten with a defined value on the next line.

It is also important to note that the uniform() function can not be implemented simply as random() % (m+1) unless a bias in the results is acceptable.

Statistics on random permutations

Fixed points

Main article: Rencontres numbers

The probability distribution of the number of fixed points of a uniformly distributed random permutation approaches a Poisson distribution with expected value 1 as n grows. In particular, it is an elegant application of the inclusion-exclusion principle to show that the probability that there are no fixed points approaches 1/e. The first n moments of this distribution are exactly those of the Poisson distribution.

Randomness testing

As with all random processes, the quality of the resulting distribution of an implementation of a randomized algorithm such as the Knuth shuffle (i.e., how close it is to the desired uniform distribution) depends on the quality of the underlying source of randomness, such as a pseudorandom number generator. There are many possible randomness tests for random permutations, such as some of the Diehard tests. A typical example of such a test is to take some permutation statistic for which the distribution is known and test whether the distribution of this statistic on a set of randomly generated permutations closely approximates the true distribution.

See also

External links