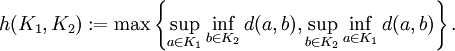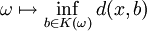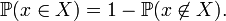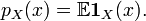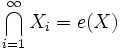Random compact set
In mathematics, a random compact set is essentially a compact set-valued random variable. Random compact sets are useful in the study of attractors for random dynamical systems.
Definition
Let 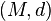 be a complete separable metric space. Let
be a complete separable metric space. Let 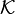 denote the set of all compact subsets of
denote the set of all compact subsets of 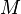 . The Hausdorff metric
. The Hausdorff metric 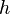 on
on 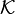 is defined by
is defined by
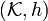 is also а complete separable metric space. The corresponding open subsets generate a σ-algebra on
is also а complete separable metric space. The corresponding open subsets generate a σ-algebra on 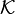 , the Borel sigma algebra
, the Borel sigma algebra 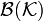 of
of 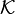 .
.
A random compact set is а measurable function  from а probability space
from а probability space 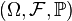 into
into 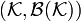 .
.
Put another way, a random compact set is a measurable function 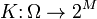 such that
such that 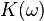 is almost surely compact and
is almost surely compact and
is a measurable function for every 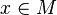 .
.
Discussion
Random compact sets in this sense are also random closed sets as in Matheron (1975). Consequently their distribution is given by the probabilities
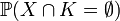 for
for 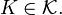
(The distribution of а random compact convex set is also given by the system of all inclusion probabilities 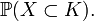 )
)
For 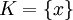 , the probability
, the probability 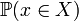 is obtained, which satisfies
is obtained, which satisfies
Thus the covering function 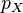 is given by
is given by
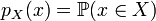 for
for 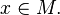
Of course, 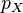 can also be interpreted as the mean of the indicator function
can also be interpreted as the mean of the indicator function 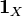 :
:
The covering function takes values between 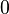 and
and 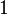 . The set
. The set 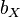 of all
of all 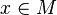 with
with 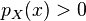 is called the support of
is called the support of  . The set
. The set 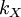 , of all
, of all 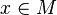 with
with 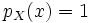 is called the kernel, the set of fixed points, or essential minimum
is called the kernel, the set of fixed points, or essential minimum 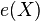 . If
. If  , is а sequence of i.i.d. random compact sets, then almost surely
, is а sequence of i.i.d. random compact sets, then almost surely
and 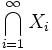 converges almost surely to
converges almost surely to 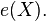
References
- Matheron, G. (1975) Random Sets and Integral Geometry. J.Wiley & Sons, New York.
- Molchanov, I. (2005) The Theory of Random Sets. Springer, New York.
- Stoyan D., and H.Stoyan (1994) Fractals, Random Shapes and Point Fields. John Wiley & Sons, Chichester, New York.