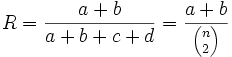Rand index
The Rand index[1] or Rand measure (named after William M. Rand) in statistics, and in particular in data clustering, is a measure of the similarity between two data clusterings. A form of the Rand index may be defined that is adjusted for the chance grouping of elements, this is the adjusted Rand index. From a mathematical standpoint, Rand index is related to the accuracy, but is applicable even when class labels are not used.
Rand index
Definition
Given a set of  elements
elements 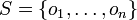 and two partitions of
and two partitions of  to compare,
to compare, 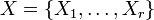 , a partition of S into r subsets, and
, a partition of S into r subsets, and 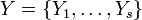 , a partition of S into s subsets, define the following:
, a partition of S into s subsets, define the following:
-
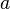 , the number of pairs of elements in
, the number of pairs of elements in  that are in the same set in
that are in the same set in  and in the same set in
and in the same set in 
-
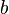 , the number of pairs of elements in
, the number of pairs of elements in  that are in different sets in
that are in different sets in  and in different sets in
and in different sets in 
-
 , the number of pairs of elements in
, the number of pairs of elements in  that are in the same set in
that are in the same set in  and in different sets in
and in different sets in 
-
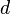 , the number of pairs of elements in
, the number of pairs of elements in  that are in different sets in
that are in different sets in  and in the same set in
and in the same set in 
Intuitively, 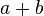 can be considered as the number of agreements between
can be considered as the number of agreements between  and
and  and
and 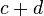 as the number of disagreements between
as the number of disagreements between  and
and  .
.
Properties
The Rand index has a value between 0 and 1, with 0 indicating that the two data clusters do not agree on any pair of points and 1 indicating that the data clusters are exactly the same.
In mathematical terms, a, b, c, d are defined as follows:
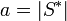 , where
, where 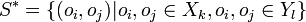
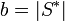 , where
, where 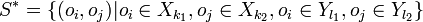
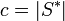 , where
, where 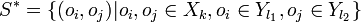
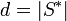 , where
, where 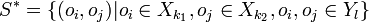
for some 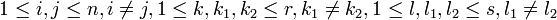
Adjusted Rand index
The adjusted Rand index is the corrected-for-chance version of the Rand index.[1][2][3] Though the Rand Index may only yield a value between 0 and +1, the Adjusted Rand Index can yield negative values if the index is less than the expected index.[4]
The contingency table
Given a set  of
of  elements, and two groupings (e.g. clusterings) of these points, namely
elements, and two groupings (e.g. clusterings) of these points, namely 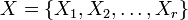 and
and 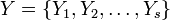 , the overlap between
, the overlap between  and
and  can be summarized in a contingency table
can be summarized in a contingency table ![\left[n_{ij}\right]](../I/m/ba8129e3338070e35d1f5cbf0a8b9c13.png) where each entry
where each entry 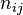 denotes the number of objects in common between
denotes the number of objects in common between 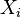 and
and 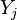 :
: 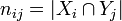 .
.
| X\Y | 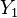 |
 |
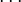 |
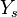 |
Sums |
|---|---|---|---|---|---|
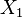 |
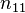 |
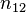 |
 |
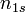 |
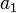 |
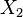 |
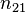 |
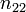 |
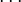 |
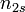 |
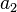 |
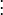 |
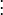 |
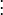 |
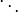 |
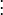 |
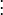 |
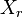 |
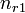 |
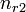 |
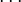 |
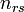 |
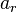 |
| Sums | 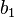 |
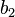 |
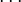 |
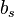 |
|
Definition
The adjusted form of the Rand Index, the Adjusted Rand Index, is 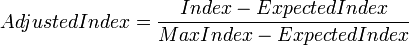 , more specifically
, more specifically
![ARI = \frac{ \sum_{ij} \binom{n_{ij}}{2} - [\sum_i \binom{a_i}{2} \sum_j \binom{b_j}{2}] / \binom{n}{2} }{ \frac{1}{2} [\sum_i \binom{a_i}{2} + \sum_j \binom{b_j}{2}] - [\sum_i \binom{a_i}{2} \sum_j \binom{b_j}{2}] / \binom{n}{2} }](../I/m/4b7ac8ac71587e88f837f319c81c7386.png)
where 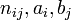 are values from the contingency table.
are values from the contingency table.
References
- ↑ 1.0 1.1 1.2 W. M. Rand (1971). "Objective criteria for the evaluation of clustering methods". Journal of the American Statistical Association (American Statistical Association) 66 (336): 846–850. doi:10.2307/2284239. JSTOR 2284239.
- ↑ 2.0 2.1 Lawrence Hubert and Phipps Arabie (1985). "Comparing partitions". Journal of Classification 2 (1): 193–218. doi:10.1007/BF01908075.
- ↑ Nguyen Xuan Vinh, Julien Epps and James Bailey (2009). PDF. "Information Theoretic Measures for Clustering Comparison: Is a Correction for Chance Necessary?". ICML '09: Proceedings of the 26th Annual International Conference on Machine Learning. ACM. pp. 1073–1080.PDF.
- ↑ http://i11www.iti.uni-karlsruhe.de/extra/publications/ww-cco-06.pdf
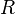 , is:
, is: