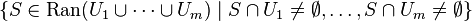Ran space
In mathematics, the Ran space (or Ran's space) of a topological space X is a topological space 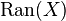 whose underlying set is the set of all nonempty finite subsets of X: for a metric space X the topology is given by Hausdorff distance. The notion is named after Ziv Ran. It seems the notion was first introduced and popularized by A. Beilinson and V. Drinfeld, Chiral algebras.
whose underlying set is the set of all nonempty finite subsets of X: for a metric space X the topology is given by Hausdorff distance. The notion is named after Ziv Ran. It seems the notion was first introduced and popularized by A. Beilinson and V. Drinfeld, Chiral algebras.
In general, the topology of the Ran space is generated by sets
for any disjoint open subsets 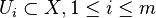 .
.
A theorem of Beilinson and Drinfeld states that the Ran space of a connected manifold is weakly contractible.[1]
There is an analog of a Ran space for a scheme:[2] the Ran prestack of a quasi-projective scheme X over a field k, denoted by 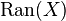 , is the category where the objects are triples
, is the category where the objects are triples 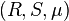 consisting of a finitely generated k-algebra R, a nonempty set S and a map of sets
consisting of a finitely generated k-algebra R, a nonempty set S and a map of sets 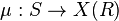 and where a morphism
and where a morphism 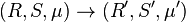 consists of a k-algebra homomorphism
consists of a k-algebra homomorphism 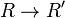 , a surjective map
, a surjective map 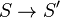 that commutes with
that commutes with  and
and 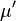 . Roughly, an R-point of
. Roughly, an R-point of 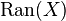 is a nonempty finite set of R-rational points of X "with labels" given by
is a nonempty finite set of R-rational points of X "with labels" given by  . A theorem of Beilinson and Drinfeld continues to hold:
. A theorem of Beilinson and Drinfeld continues to hold: 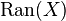 is acyclic if X is connected.
is acyclic if X is connected.
Topological chiral homology
If F is a cosheaf on the Ran space 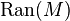 , then its space of global sections is called the topological chiral homology of M with coefficients in F. If A is, roughly, a family of commutative algebras parametrized by points in M, then there is a factorizable sheaf associated to A. Via this construction, one also obtains the topological chiral homology with coefficients in A. The construction is a generalization of Hochschild homology.[3]
, then its space of global sections is called the topological chiral homology of M with coefficients in F. If A is, roughly, a family of commutative algebras parametrized by points in M, then there is a factorizable sheaf associated to A. Via this construction, one also obtains the topological chiral homology with coefficients in A. The construction is a generalization of Hochschild homology.[3]
See also
- Chiral homology
- Exponential space
Notes
- ↑ Lurie 2012, Theorem 5.3.1.6.
- ↑ http://www.math.harvard.edu/~lurie/282ynotes/LectureVII-Stacks.pdf
- ↑ Lurie 2012, Theorem 5.3.3.11
References
- D. Gaitsgory, Contractibility of the space of rational maps, 2012
- http://www.math.harvard.edu/~lurie/282ynotes/LectureVIII-Poincare.pdf
- J. Lurie, Higher Algebra, last updated August 2012
- http://pantodon.shinshu-u.ac.jp/topology/literature/ja/exponential_space.html