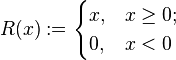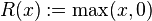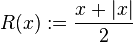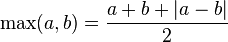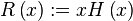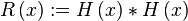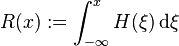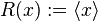Ramp function

Graph of the ramp function

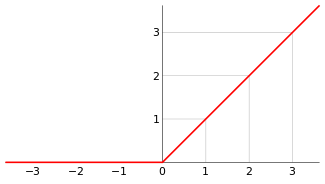
The ramp function is a unary real function, easily computable as the mean of the independent variable and its absolute value.

This function is applied in engineering (e.g., in the theory of DSP). The name ramp function is derived from the appearance of its graph.

Definitions

The ramp function (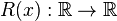 $R(x): \mathbb{R} \rightarrow \mathbb{R}$ ) may be defined analytically in several ways. Possible definitions are:

R(x) := \begin{cases} x, & x \ge 0; \\ 0, & x<0 \end{cases}

or

R(x) := \operatorname{max}(x,0)

The mean of a straight line with unity gradient and its modulus:

R(x) := \frac{x+|x|}{2}

this can be derived by noting the following definition of 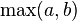$\operatorname{max}(a,b)$ ,

\operatorname{max}(a,b) = \frac{a+b+|a-b|}{2}

for which $a = x$ and $b = 0$

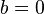
The Heaviside step function multiplied by a straight line with unity gradient:

R\left( x \right) := xH\left( x \right)

The convolution of the Heaviside step function with itself:

R\left( x \right) := H\left( x \right) * H\left( x \right)

The integral of the Heaviside step function:

R(x) := \int_{-\infty}^{x} H(\xi)\,\mathrm{d}\xi

Macaulay brackets:

R(x) := \langle x\rangle

Analytic properties

Non-negativity

In the whole domain the function is non-negative, so its absolute value is itself, i.e.

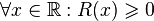
$\forall x \in \mathbb{R}: R(x) \geqslant 0$

and

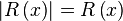
$\left| R \left( x \right) \right| = R\left( x \right)$

Proof: by the mean of definition [2] it is non-negative in the I. quarter, and zero in the II.; so everywhere it is non-negative.

Derivative

Its derivative is the Heaviside function:

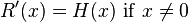
$R'(x) = H(x)\ \mathrm{if}\ x \ne 0$

From this property definition [5]. goes.

Fourier transform

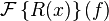
\mathcal{F}\left\{ R(x) \right\}(f)

=

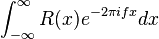
\int_{-\infty}^{\infty}R(x) e^{-2\pi ifx}dx

=

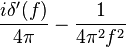
\frac{i\delta '(f)}{4\pi}-\frac{1}{4\pi^{2}f^{2}}

Where δ(x) is the Dirac delta (in this formula, its derivative appears).

Laplace transform

The single-sided Laplace transform of $R(x)$ is given as follows,

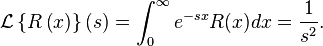
\mathcal{L}\left\{ R\left( x \right)\right\} (s) = \int_{0}^{\infty} e^{-sx}R(x)dx = \frac{1}{s^2}.

Algebraic properties

Iteration invariance

Every iterated function of the ramp mapping is itself, as

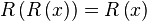R \left( R \left( x \right) \right) = R \left( x \right)

.

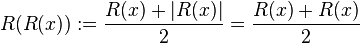
Proof: $R(R(x)):= \frac{R(x)+|R(x)|}{2} = \frac{R(x)+R(x)}{2}$ $=$
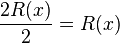$=$ $\frac{2R(x)}{2} = R(x)$ .

We applied the non-negative property.

References

Mathworld