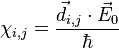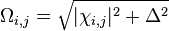Rabi frequency

The Rabi frequency is the frequency of oscillation for a given atomic transition in a given light field. It also gives the measure of the fluctuation of population between the levels. It is associated with the strength of the coupling between the light and the transition. Rabi flopping between the levels of a 2-level system illuminated with resonant light, will occur at the Rabi frequency. The Rabi frequency is a semiclassical concept as it is based on a quantum atomic transition and a classical light field.

In the context of a nuclear magnetic resonance experiment, the Rabi frequency is the nutation frequency of a sample's net nuclear magnetization vector about a radiofrequency field. (Note that this is distinct from the Larmor frequency, which characterizes the precession of a transverse nuclear magnetization about a static magnetic field.)

Definition

The Rabi frequency is defined as

\chi_{i,j} = {\vec{d}_{i,j}\cdot\vec{E}_0 \over \hbar}

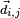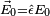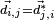where \scriptstyle{\vec{d}_{i,j}} is the transition dipole moment for the \scriptstyle{i \rightarrow j} transition and \scriptstyle{\vec{E}_0 = \hat{\epsilon}E_0} is the vector electric field amplitude which includes the polarization. The numerator has dimensions of energy, so dividing by \scriptstyle{\hbar} gives an angular frequency. 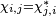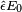Although \scriptstyle{\vec{d}_{i,j} = \vec{d}_{j,i}^*}, one cannot assume that \scriptstyle{\chi_{i,j} = \chi_{j,i}^*} as \scriptstyle{\hat{\epsilon}E_0} may be complex, as in the case of circularly polarized light.[1]

By analogy with a classical dipole, it is clear that an atom with a large dipole moment will be more susceptible to perturbation by electric and magnetic fields. The dot product includes a factor of 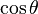\cos\theta, where \theta is the angle between the polarization of the light and the transition dipole moment. When they are parallel or antiparallel the interaction is strongest, when they are perpendicular there is no interaction at all. The vector electric field amplitude defines both the intensity and the polarization of the light.

In real systems, with more than two levels, the correct dipole transition matrix element for the relevant transition has to be calculated. When equating the Rabi frequency the correct Clebsch-Gordan coefficient has to be considered which is a common source of mistakes throughout scientific literature. There are also some publications that use a different definition for the Rabi frequency which is by a factor of two smaller than the one introduced here.

Generalized Rabi frequency

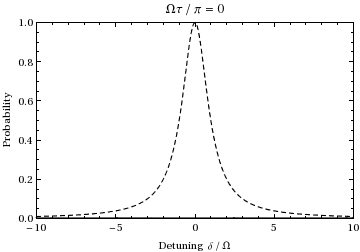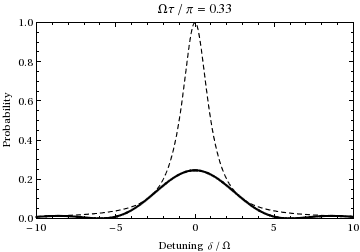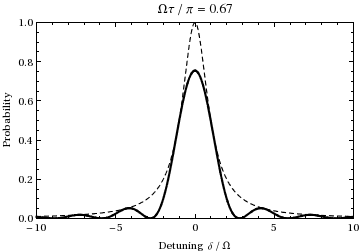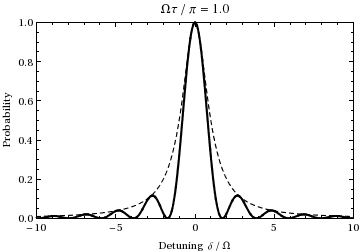
For light that is off resonance with a transition, it is common to define the generalized Rabi frequency 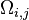\Omega_{i,j}. Rabi flopping actually occurs at the generalized Rabi frequency.

\Omega_{i,j} = \sqrt{|\chi_{i,j}|^2 + \Delta^2}

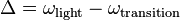where \Delta = \omega_\text{light} - \omega_\text{transition} is the detuning, a measure of how far the light is off resonance with the transition.

See also

References

  1. ↑ Milonni, Peter W.; Eberly, Joseph H. (1998). Lasers. John Wiley & Sons. p. 191. ISBN 0-471-62731-3.