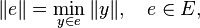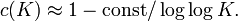Quotient of subspace theorem

In mathematics, the quotient of subspace theorem is an important property of finite-dimensional normed spaces, discovered by Vitali Milman.^[1]

Let (X, ||·||) be an N-dimensional normed space. There exist subspaces Z ⊂ Y ⊂ X such that the following holds:

The quotient space E = Y / Z is of dimension dim E ≥ c N, where c > 0 is a universal constant.
The induced norm || · || on E, defined by

\| e \| =\min_{y \in e} \| y \|, \quad e \in E,

is uniformly isomorphic to Euclidean. That is, there exists a positive quadratic form ("Euclidean structure") Q on E, such that

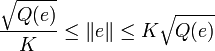\frac{\sqrt{Q(e)}}{K} \leq \| e \| \leq K \sqrt{Q(e)}

for

e \in E,

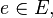
with K > 1 a universal constant.

The statement is relative easy to prove by induction on the dimension of Z (even for Y=Z, X=0, c=1) with a K that depends only on N; the point of the theorem is that K is independent of N.

In fact, the constant c can be made arbitrarily close to 1, at the expense of the constant K becoming large. The original proof allowed

c(K) \approx 1 - \text{const} / \log \log K.

^[2]

Notes

↑ The original proof appeared in Milman (1984). See also Pisier (1989).
↑ See references for improved estimates.

References

Milman, V.D. (1984), "Almost Euclidean quotient spaces of subspaces of a finite-dimensional normed space", Israel seminar on geometrical aspects of functional analysis (Tel Aviv: Tel Aviv Univ.) X
Gordon, Y. (1988), "On Milman's inequality and random subspaces which escape through a mesh in Rⁿ", Geometric aspects of functional analysis, Lecture Notes in Math. (Berlin: Springer) 1317: 84–106, doi:10.1007/BFb0081737, ISBN 978-3-540-19353-1
Pisier, G. (1989), The volume of convex bodies and Banach space geometry, Cambridge Tracts in Mathematics 94, Cambridge: Cambridge University Press