Quickhull

Quickhull is a method of computing the convex hull of a finite set of points in the plane. It uses a divide and conquer approach similar to that of quicksort, which its name derives from. Its average case complexity is considered to be O(n * log(n)), whereas in the worst case it takes O(n²) (quadratic).

This animation depicts the quickhull algorithm.

Algorithm

Steps 1-2: Divide points in two subsets

Under average circumstances the algorithm works quite well, but processing usually becomes slow in cases of high symmetry or points lying on the circumference of a circle. The algorithm can be broken down to the following steps:

1. Find the points with minimum and maximum x coordinates, those are bound to be part of the convex hull.
2. Use the line formed by the two points to divide the set in two subsets of points, which will be processed recursively.
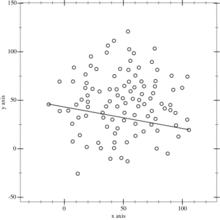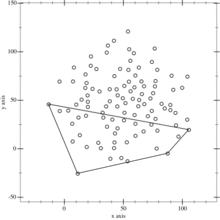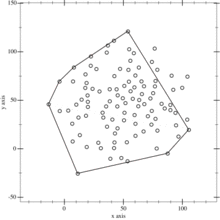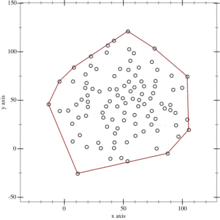
3. Determine the point, on one side of the line, with the maximum distance from the line. The two points found before along with this one form a triangle.
4. The points lying inside of that triangle cannot be part of the convex hull and can therefore be ignored in the next steps.
5. Repeat the previous two steps on the two lines formed by the triangle (not the initial line).
6. Keep on doing so on until no more points are left, the recursion has come to an end and the points selected constitute the convex hull.

Steps 3-5: Find maximal distance point, ignore points inside triangle and repeat it

Step 6: Recurse until no more points are left

Alternative algorithm

This is a minor change towards the initial steps of the algorithm which might help save some computation time. One can note that the points with minimum and maximum y coordinates are also bound to be part of the convex hull, therefore, there are four points (or less depending on whether these points are the same or different) which are bound to be part of the convex hull. It is possible to discard directly all points lying inside the quadrilateral found within these four points (or less). Also, a first check needs to be made to check the number of points at start, if there are only three points, then the algorithm can be solved in O(1) since the three points are part of the convex hull.

The algorithm can be broken down to the following steps:

1. If the set of point is of size 3, then the three points are part of the convex hull and the algorithm can be ended.
2. Find the points with minimum and maximum x coordinates and with minimum and maximum y coordinates, those are bound to be part of the convex hull.
3. The points lying inside of the quadrilateral formed by the previous extrema cannot be part of the convex hull and can therefore be ignored in the next steps.
4. Use the line formed by a pair of extrema from step two to divide the remaining set in two subsets of points, which will be processed recursively.
5. Determine the point, on one side of the line, with the maximum distance from the line. The two points found before along with this one form a triangle.
6. The points lying inside of that triangle cannot be part of the convex hull and can therefore be ignored in the next steps.
7. Repeat the previous two steps on the two lines formed by the triangle (not the initial line).
8. Keep on doing so on until no more points are left, the recursion has come to an end and the points selected constitute the convex hull.

References

• Barber, C. Bradford; Dobkin, David P.; Huhdanpaa, Hannu (1 December 1996). "The quickhull algorithm for convex hulls". ACM Transactions on Mathematical Software 22 (4): 469–483. doi:10.1145/235815.235821. 
• Dave Mount. "Lecture 3: More Convex Hull Algorithms".