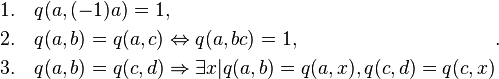Quaternionic structure
In mathematics, a quaternionic structure or Q-structure is an axiomatic system that abstracts the concept of a quaternion algebra over a field.
A quaternionic structure is a triple (G,Q,q) where G is an elementary abelian group of exponent 2 with a distinguished element −1, Q is a pointed set with distinguished element 1, and q is a symmetric surjection G×G → Q satisfying axioms
Every field F gives rise to a Q-structure by taking G to be F∗/F∗2, Q the set of Brauer classes of quaternion algebras in the Brauer group of F with the split quaternion algebra as distinguished element and q(a,b) the quaternion algebra (a,b)F.
References
- Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics 67. American Mathematical Society. ISBN 0-8218-1095-2. MR 2104929. Zbl 1068.11023.