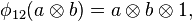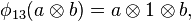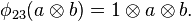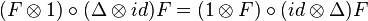Quasitriangular Hopf algebra

In mathematics, a Hopf algebra, H, is quasitriangular^[1] if there exists an invertible element, R, of 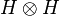$H \otimes H$ such that

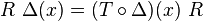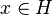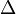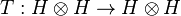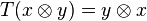$R \ \Delta(x) = (T \circ \Delta)(x) \ R$ for all $x \in H$ , where $\Delta$ is the coproduct on H, and the linear map $T : H \otimes H \to H \otimes H$ is given by $T(x \otimes y) = y \otimes x$ ,

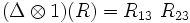$(\Delta \otimes 1)(R) = R_{13} \ R_{23}$ ,

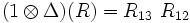$(1 \otimes \Delta)(R) = R_{13} \ R_{12}$ ,

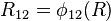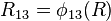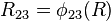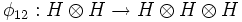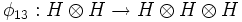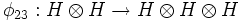where $R_{12} = \phi_{12}(R)$ , $R_{13} = \phi_{13}(R)$ , and $R_{23} = \phi_{23}(R)$ , where $\phi_{12} : H \otimes H \to H \otimes H \otimes H$ , $\phi_{13} : H \otimes H \to H \otimes H \otimes H$ , and $\phi_{23} : H \otimes H \to H \otimes H \otimes H$ , are algebra morphisms determined by

\phi_{12}(a \otimes b) = a \otimes b \otimes 1,

\phi_{13}(a \otimes b) = a \otimes 1 \otimes b,

\phi_{23}(a \otimes b) = 1 \otimes a \otimes b.

R is called the R-matrix.

As a consequence of the properties of quasitriangularity, the R-matrix, R, is a solution of the Yang-Baxter equation (and so a module V of H can be used to determine quasi-invariants of braids, knots and links). 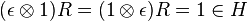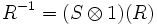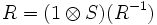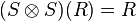Also as a consequence of the properties of quasitriangularity, $(\epsilon \otimes 1) R = (1 \otimes \epsilon) R = 1 \in H$ ; moreover $R^{-1} = (S \otimes 1)(R)$ , $R = (1 \otimes S)(R^{-1})$ , and $(S \otimes S)(R) = R$ . One may further show that the antipode S must be a linear isomorphism, and thus S² is an automorphism. 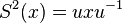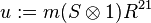In fact, S² is given by conjugating by an invertible element: $S^2(x)= u x u^{-1}$ where $u := m (S \otimes 1)R^{21}$ (cf. Ribbon Hopf algebras).

It is possible to construct a quasitriangular Hopf algebra from a Hopf algebra and its dual, using the Drinfeld quantum double construction.

Twisting

The property of being a quasi-triangular Hopf algebra is preserved by twisting via an invertible element 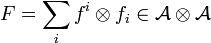$F = \sum_i f^i \otimes f_i \in \mathcal{A \otimes A}$ such that $(\varepsilon \otimes id )F = (id \otimes \varepsilon)F = 1$ and satisfying the cocycle condition

(F \otimes 1) \circ (\Delta \otimes id) F = (1 \otimes F) \circ (id \otimes \Delta) F

Furthermore, 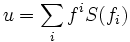$u = \sum_i f^i S(f_i)$ is invertible and the twisted antipode is given by 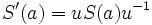$S'(a) = u S(a)u^{-1}$ , with the twisted comultiplication, R-matrix and co-unit change according to those defined for the quasi-triangular Quasi-Hopf algebra. Such a twist is known as an admissible (or Drinfeld) twist.

Notes

↑ Montgomery & Schneider (2002), p. 72.

References

Montgomery, Susan (1993). Hopf algebras and their actions on rings. Regional Conference Series in Mathematics 82. Providence, RI: American Mathematical Society. ISBN 0-8218-0738-2. Zbl 0793.16029.
Montgomery, Susan; Schneider, Hans-Jürgen (2002). New directions in Hopf algebras. Mathematical Sciences Research Institute Publications 43. Cambridge University Press. ISBN 978-0-521-81512-3. Zbl 0990.00022.

Quasitriangular Hopf algebra

Twisting

See also

Notes

References