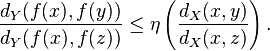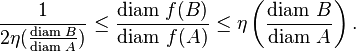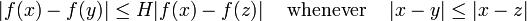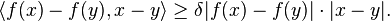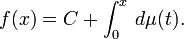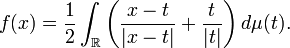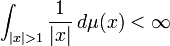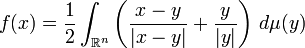Quasisymmetric map

For quasisymmetric functions in algebraic combinatorics, see quasisymmetric function.

In mathematics, a quasisymmetric homeomorphism between metric spaces is a map that generalizes bi-Lipschitz maps. While bi-Lipschitz maps shrink or expand the diameter of a set by no more than a multiplicative factor, quasisymmetric maps satisfy the weaker geometric property that they preserve the relative sizes of sets: if two sets A and B have diameters t and are no more than distance t apart, then the ratio of their sizes changes by no more than a multiplicative constant. These maps are also related to quasiconformal maps, since in many circumstances they are in fact equivalent.[1]

Definition

Let (X, dX) and (Y, dY) be two metric spaces. A homeomorphism f:X → Y is said to be η-quasisymmetric if there is an increasing function η : [0, ∞) → [0, ∞) such that for any triple x, y, z of distinct points in X, we have

\frac{d_Y(f(x),f(y))}{d_{Y}(f(x),f(z))} \leq \eta\left(\frac{d_X(x,y)}{d_X(x,z)}\right).

Basic properties

Inverses are quasisymmetric 
If f : X → Y is an invertible η-quasisymmetric map as above, then its inverse map is ή-quasisymmetric, where ή(t) = 1/η(1/t).
Quasisymmetric maps preserve relative sizes of sets 
If A and B are subsets of X and A is a subset of B, then
\frac{1}{2\eta(\frac{\text{diam }B}{\text{diam }A})}\leq \frac{\text{diam }f(B)}{\text{diam }f(A)}\leq \eta\left(\frac{\text{diam }B}{\text{diam }A}\right).

Examples

Weakly quasisymmetric maps

A map f:X→Y is said to be H-weakly-quasisymmetric for some H > 0 if for all triples of distinct points x,y,z in X, we have

|f(x)-f(y)|\leq H|f(x)-f(z)|\;\;\;\text{ whenever }\;\;\; |x-y|\leq |x-z|

Not all weakly quasisymmetric maps are quasisymmetric. However, if X is connected and doubling, then all weakly quasisymmetric maps are quasisymmetric. The appeal of this result is that proving weak-quasisymmetry is much easier than proving quasisymmetry directly, and in many natural settings we have the luck of knowing the two are equivalent.

δ-monotone maps

A monotone map f:H → H on a Hilbert space H is δ-monotone if for all x and y in H,

\langle f(x)-f(y),x-y\rangle\geq \delta |f(x)-f(y)|\cdot|x-y|.

To grasp what this condition means geometrically, suppose f(0) = 0 and consider the above estimate when y = 0. Then it implies that the angle between the vector x and its image f(x) stays between 0 and arccos δ < π/2.

These maps are quasisymmetric, although they are a much narrower subclass of quasisymmetric maps. For example, while a general quasisymmetric map in the complex plane could map the real line to a set of Hausdorff dimension strictly greater than one, a δ-monotone will always map the real line to a rotated graph of a Lipschitz function L:ℝ → ℝ.[2]

Quasisymmetric maps and doubling measures

The real line

Quasisymmetric homeomorphisms of the real line to itself can be characterized in terms of their derivatives.[3] An increasing homeomorphism f:ℝ → ℝ is quasisymmetric if and only if there is a constant C > 0 and a doubling measure μ on the real line such that

f(x)=C+\int_0^x \, d\mu(t).

Euclidean space

An analogous result holds in Euclidean space. Suppose C = 0 and we rewrite the above equation for f as

f(x) = \frac{1}{2}\int_{\mathbb{R}}\left(\frac{x-t}{|x-t|}+\frac{t}{|t|}\right)d\mu(t).

Writing it this way, we can attempt to define a map using this same integral, but instead integrate (what is now a vector valued integrand) over ℝn: if μ is a doubling measure on ℝn and

\int_{|x|>1}\frac{1}{|x|}\,d\mu(x)<\infty

then the map

f(x) = \frac{1}{2}\int_{\mathbb{R}^{n}}\left(\frac{x-y}{|x-y|}+\frac{y}{|y|}\right)\,d\mu(y)

is quasisymmetric (in fact, it is δ-monotone for some δ depending on the measure μ).[4]

Quasisymmetry and quasiconformality in Euclidean space

Let Ω and Ω´ be open subsets of ℝn. If f : Ω → Ω´ is η-quasisymmetric, then it is also K-quasiconformal, where K > 0 is a constant depending on η.

Conversely, if f : Ω → Ω´ is K-quasiconformal and B(x, 2r) is contained in Ω, then f is η-quasisymmetric on B(x, r), where η depends only on K.

References

  1. ↑ Heinonen, Juha (2001). Lectures on Analysis on Metric Spaces. Universitext. New York: Springer-Verlag. pp. x+140. ISBN 0-387-95104-0.
  2. ↑ Kovalev, Leonid V. (2007). "Quasiconformal geometry of monotone mappings". Journal of the London Mathematical Society 75 (2): 391–408. doi:10.1112/jlms/jdm008.
  3. ↑ Beurling, A.; Ahlfors, L. (1956). "The boundary correspondence under quasiconformal mappings". Acta Math. 96: 125–124. doi:10.1007/bf02392360.
  4. ↑ Kovalev, Leonid; Maldonado, Diego; Wu, Jang-Mei (2007). "Doubling measures, monotonicity, and quasiconformality". Math. Z. 257 (3): 525–545. arXiv:math/0611110. doi:10.1007/s00209-007-0132-5.