Quasisymmetric function
In algebra and in particular in algebraic combinatorics, a quasisymmetric function is any element in the ring of quasisymmetric functions which is in turn a subring of the formal power series ring with a countable number of variables. This ring generalizes the ring of symmetric functions. This ring can be realized as a specific limit of the rings of quasisymmetric polynomials in n variables, as n goes to infinity. This ring serves as universal structure in which relations between quasisymmetric polynomials can be expressed in a way independent of the number n of variables (but its elements are neither polynomials nor functions).
Definitions
The ring of quasisymmetric functions, denoted QSym, can be defined over any commutative ring R such as the integers.
Quasisymmetric
functions are power series of bounded degree in variables 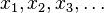 with coefficients in R, which are shift invariant in the sense that the coefficient of the monomial
with coefficients in R, which are shift invariant in the sense that the coefficient of the monomial 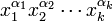 is equal to the coefficient of the monomial
is equal to the coefficient of the monomial 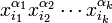 for any strictly increasing sequence of positive integers
for any strictly increasing sequence of positive integers
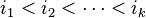 indexing the variables and any positive integer sequence
indexing the variables and any positive integer sequence 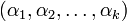 of exponents.[1]
Much of the study of quasisymmetric functions is based on that of symmetric functions.
of exponents.[1]
Much of the study of quasisymmetric functions is based on that of symmetric functions.
A quasisymmetric function in finitely many variables is a quasisymmetric polynomial.
Both symmetric and quasisymmetric polynomials may be characterized in terms of actions of the symmetric group 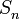 on a polynomial ring in
on a polynomial ring in 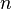 variables
variables 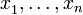 .
One such action of
.
One such action of 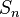 permutes variables,
changing a polynomial
permutes variables,
changing a polynomial 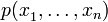 by iteratively swapping pairs
by iteratively swapping pairs 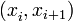 of variables having consecutive indices.
Those polynomials unchanged by all such swaps
form the subring of symmetric polynomials.
A second action of
of variables having consecutive indices.
Those polynomials unchanged by all such swaps
form the subring of symmetric polynomials.
A second action of 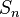 conditionally permutes variables,
changing a polynomial
conditionally permutes variables,
changing a polynomial 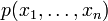 by swapping pairs
by swapping pairs 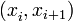 of variables
except in monomials containing both variables.
Those polynomials unchanged by all such conditional swaps form
the subring of quasisymmetric polynomials. One quasisymmetric function in four variables is the polynomial
of variables
except in monomials containing both variables.
Those polynomials unchanged by all such conditional swaps form
the subring of quasisymmetric polynomials. One quasisymmetric function in four variables is the polynomial
The simplest symmetric function containing all of these monomials is
Important bases
QSym is a graded R-algebra, decomposing as
where 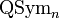 is the
is the  -span of all quasisymmetric functions that are homogeneous of degree
-span of all quasisymmetric functions that are homogeneous of degree  . Two natural bases for
. Two natural bases for 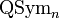 are the monomial basis
are the monomial basis 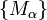 and the fundamental basis
and the fundamental basis 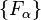 indexed by compositions
indexed by compositions 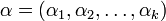 of
of  , denoted
, denoted 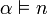 . The monomial basis consists of
. The monomial basis consists of 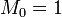 and all formal power series
and all formal power series
The fundamental basis consists 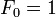 and all formal power series
and all formal power series
where 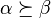 means we can obtain
means we can obtain  by adding together adjacent parts of
by adding together adjacent parts of  , for example, (3,2,4,2)
, for example, (3,2,4,2)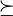 (3,1,1,1,2,1,2). Thus, when the ring
(3,1,1,1,2,1,2). Thus, when the ring  is the ring of rational numbers, one has
is the ring of rational numbers, one has
Then one can define the algebra of symmetric functions 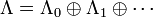 as the subalgebra of QSym spanned by the monomial symmetric functions
as the subalgebra of QSym spanned by the monomial symmetric functions 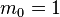 and all formal power series
and all formal power series 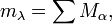 where the sum is over all compositions
where the sum is over all compositions  which rearrange to the partition
which rearrange to the partition  . Moreover, we have
. Moreover, we have 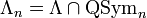 . For example,
. For example, 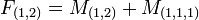 and
and 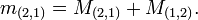
Other important bases for quasisymmetric functions include the basis of quasisymmetric Schur functions,[2] and bases related to enumeration in matroids.[3][4]
Applications
Quasisymmetric functions have been applied in enumerative combinatorics, symmetric function theory, representation theory, and number theory. Applications of quasisymmetric functions include enumeration of P-partitions,[5][6] permutations,[7][8][9][10] tableaux,[11] chains of posets,[11][12] reduced decompositions in finite Coxeter groups (via Stanley symmetric functions),[11] and parking functions.[13] In symmetric function theory and representation theory, applications include the study of Schubert polynomials,[14][15] Macdonald polynomials,[16] Hecke algebras,[17] and Kazhdan-Lusztig polynomials.[18] Often quasisymmetric functions provide a powerful bridge between combinatorial structures and symmetric functions.
Related algebras
As a graded Hopf algebra, the dual of the ring of quasisymmetric functions is the ring of noncommutative symmetric functions. Every symmetric function is also a quasisymmetric function, and hence the ring of symmetric functions is a subalgebra of the ring of quasisymmetric functions.
The ring of quasisymmetric functions is the terminal object in category of graded Hopf algebras with a single character.[19] Hence any such Hopf algebra has a morphism to the ring of quasisymmetric functions.
One example of this is the peak algebra.[20]
Other Related Algebras: The Malvenuto-Reutenauer algebra[21] is a Hopf algebra based on permutations that relates the rings of symmetric functions, quasisymmetric functions, and noncommutative symmetric functions, (denoted Sym, QSym, and NSym respectively), as depicted the following commutative diagram. The duality between QSym and NSym mentioned above is reflected in the main diagonal of this diagram.
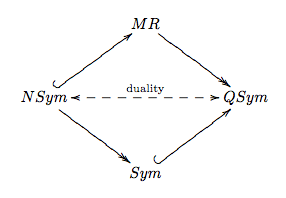
Many related Hopf algebras were constructed from Hopf monoids in the category of species by Aguiar and Majahan .[22]
One can also construct the ring of quasisymmetric functions in noncommuting variables.[23][24]
External links
References
- ↑ Stanley, Richard P. Enumerative Combinatorics, Vol. 2, Cambridge University Press, 1999. ISBN 0-521-56069-1 (hardback) ISBN 0-521-78987-7 (paperback).
- ↑ Haglund, J.; Luoto, K.; Mason, S.; van Willigenburg, S. (2011), "Quasisymmetric Schur functions", J. Combin. Theory Ser. A 118 (2): 463–490, doi:10.1016/j.jcta.2009.11.002
- ↑ Luoto, K. (2008), "A matroid-friendly basis for the quasisymmetric functions", J. Combin. Theory Ser. A 115 (5): 777–798, arXiv:0704.0836, Bibcode:2007arXiv0704.0836L, doi:10.1016/j.jcta.2007.10.003
- ↑ Billera, L.; Jia, N.; Reiner, V. (2009), "A quasisymmetric function for matroids", European J. Combin. 30 (8): 1727–1757, arXiv:math/0606646, Bibcode:2006math......6646B, doi:10.1016/j.ejc.2008.12.007
- ↑ Stanley, Richard P. Ordered structures and partitions, Memoirs of the American Mathematical Society, No. 119, American Mathematical Society, 1972.
- ↑ Gessel, Ira. Multipartite P-partitions and inner products of skew Schur functions, Combinatorics and algebra (Boulder, Colo., 1983), 289–317, Contemp. Math., 34, Amer. Math. Soc., Providence, RI, 1984.
- ↑ Gessel, Ira; Reutenauer, Christophe (1993), "Counting permutations with given cycle structure and descent set", J. Combin. Theory Ser. A 64 (2): 189–215, doi:10.1016/0097-3165(93)90095-P
- ↑ Hyatt, Matthew (2010), Eulerian quasisymmetric functions for the type B Coxeter group and other wreath product groups 1007, p. 459, arXiv:1007.0459, Bibcode:2010arXiv1007.0459H
- ↑ 11.0 11.1 11.2 Stanley, Richard P. (1984), "On the number of reduced decompositions of elements of Coxeter groups", European J. Combin. 5 (4): 359–372, doi:10.1016/s0195-6698(84)80039-6
- ↑ Ehrenborg, Richard (1996), "On posets and Hopf algebras", Adv. Math. 119 (1): 1–25, doi:10.1006/aima.1996.0026
- ↑ Haglund, James; The q,t-Catalan numbers and the space of diagonal harmonics. University Lecture Series, 41. American Mathematical Society, Providence, RI, 2008. viii+167 pp. ISBN 978-0-8218-4411-3; 0-8218-4411-3
- ↑ Billey, Sara C.; Jockusch, William; Stanley, Richard P. (1993), "Some combinatorial properties of Schubert polynomials", Journal of Algebraic Combinatorics 2 (4): 345–374, doi:10.1023/A:1022419800503
- ↑ Fomin, Sergey; Stanley, Richard P. (1994), "Schubert polynomials and the nil-Coxeter algebra", Advances in Mathematics 103 (2): 196–207, doi:10.1006/aima.1994.1009
- ↑ Assaf, Sami, Dual Equivalence Graphs I: A combinatorial proof of LLT and Macdonald positivity, arXiv:1005.3759, Bibcode:2010arXiv1005.3759A
- ↑ Duchamp, Gérard; Krob, Daniel; Leclerc, Bernard; Thibon, Jean-Yves (1996), "Fonctions quasi-symétriques, fonctions symétriques non commutatives et algèbres de Hecke à
 ", C. R. Acad. Sci. Paris, Sér. I Math. 322 (2): 107–112
", C. R. Acad. Sci. Paris, Sér. I Math. 322 (2): 107–112 - ↑ Billera, Louis J.; Brenti, Francesco (2007), Quasisymmetric functions and Kazhdan-Lusztig polynomials 0710, p. 3965, arXiv:0710.3965, Bibcode:2007arXiv0710.3965B
- ↑ Aguiar, Marcelo; Bergeron, Nantel; Sottile, Frank (2006), "Combinatorial Hopf algebras and generalized Dehn-Sommerville relations", Compositio Mathematica 142 (1): 1–30, arXiv:math/0310016, Bibcode:2003math.....10016A, doi:10.1112/S0010437X0500165X
- ↑ Stembridge, John R. (1997), "Enriched P-partitions", Trans. Amer. Math. Soc. 349 (2): 763–788, doi:10.1090/S0002-9947-97-01804-7
- ↑ Malvenuto, Clauda; Reutenauer, Christophe (1995), "Duality between quasi-symmetric functions and the Solomon descent algebra", Journal of Algebra 177 (3): 967–982, doi:10.1006/jabr.1995.1336
- ↑ Aguiar, Marcelo; Mahajan, Swapneel Monoidal Functors, Species and Hopf Algebras CRM Monograph Series, no. 29. American Mathematical Society, Providence, RI, 2010.
- ↑ Hivert, Florent, Ph.D. Thesis, Marne-la-Vallée
- ↑ Bergeron, Nantel; Zabrocki, Mike (2009), "The Hopf algebras of symmetric functions and quasi-symmetric functions in non-commutative variables are free and co-free", J. Algebra Appl. 8 (4): 581–600, doi:10.1142/S0219498809003485
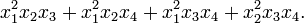
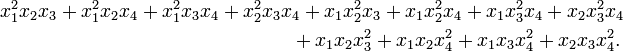
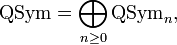
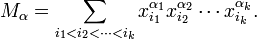
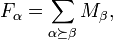
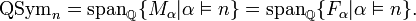
 -Eulerian polynomials: excedance number and major index", Electron. Res. Announc. Amer. Math. Soc. 13 (4): 33–45,
-Eulerian polynomials: excedance number and major index", Electron. Res. Announc. Amer. Math. Soc. 13 (4): 33–45,