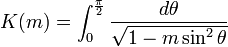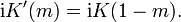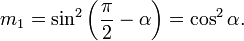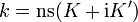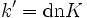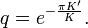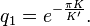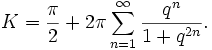Quarter period
In mathematics, the quarter periods K(m) and iK ′(m) are special functions that appear in the theory of elliptic functions.
The quarter periods K and iK ′ are given by
and
When m is a real number, 0 ≤ m ≤ 1, then both K and K ′ are real numbers. By convention, K is called the real quarter period and iK ′ is called the imaginary quarter period. Any one of the numbers m, K, K ′, or K ′/K uniquely determines the others.
These functions appear in the theory of Jacobian elliptic functions; they are called quarter periods because the elliptic functions 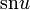 and
and 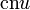 are periodic functions with periods
are periodic functions with periods 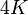 and
and 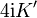 .
.
The quarter periods are essentially the elliptic integral of the first kind, by making the substitution 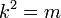 . In this case, one writes
. In this case, one writes 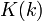 instead of
instead of 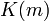 , understanding the difference between the two depends notationally on whether
, understanding the difference between the two depends notationally on whether 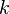 or
or 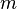 is used. This notational difference has spawned a terminology to go with it:
is used. This notational difference has spawned a terminology to go with it:
-
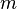 is called the parameter
is called the parameter -
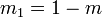 is called the complementary parameter
is called the complementary parameter -
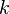 is called the elliptic modulus
is called the elliptic modulus -
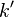 is called the complementary elliptic modulus, where
is called the complementary elliptic modulus, where 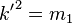
-
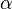 the modular angle, where
the modular angle, where 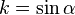
-
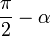 the complementary modular angle. Note that
the complementary modular angle. Note that
The elliptic modulus can be expressed in terms of the quarter periods as
and
where ns and dn Jacobian elliptic functions.
The nome 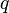 is given by
is given by
The complementary nome is given by
The real quarter period can be expressed as a Lambert series involving the nome:
Additional expansions and relations can be found on the page for elliptic integrals.
References
- Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. See chapters 16 and 17.