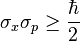Quantum topology
Quantum topology is a branch of mathematics that connects quantum mechanics with low-dimensional topology.
Dirac notation provides a viewpoint of quantum mechanics which becomes amplified into a framework that can embrace the amplitudes associated with topological spaces and the related embedding of one space within another such as knots and links in three-dimensional space. This bra–ket notation of kets and bras can be generalised, becoming maps of vector spaces associated with topological spaces that allow tensor products.[1]
Topological entanglement involving linking and braiding can be intuitively related to quantum entanglement.[1]
See also
References
- Quantum topology by Louis H. Kauffman and Randy A. Baadhio, World Scientific Publishing Co Pte Ltd, 1993
External links
- Quantum Topology at EMS Publishing House.