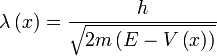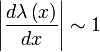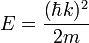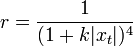Quantum reflection
Quantum reflection is a physical phenomenon involving the reflection of a matter wave from an attractive potential. In classical mechanics, such a phenomenon is not possible; for instance when one magnet is pulled toward another, the observer does not expect one of the magnets to suddenly (i.e. before the magnets 'touch') turn around and retreat in the opposite direction.
Definition
Quantum reflection became an important branch of physics in the 21st century. In a workshop about quantum reflection,[1] the following definition of quantum reflection was suggested:
Quantum reflection is a classically counterintuitive phenomenon whereby the motion of particles is reverted "against the force" acting on them. This effect manifests the wave nature of particles and influences collisions of ultracold atoms and interaction of atoms with solid surfaces.
Observation of quantum reflection has become possible thanks to recent advances in trapping and cooling atoms.
Reflection of slow atoms
Although the principles of quantum mechanics apply to any particles, usually the term "quantum reflection" means reflection of atoms from a surface of condensed matter (liquid or solid). The full potential experienced by the incident atom does become repulsive at a very small distance from the surface (of order of size of atoms). This is when the atom becomes aware of the discrete character of material. This repulsion is responsible for the classical scattering one would expect for particles incident on a surface. Such scattering is diffuse rather than specular, and so this component of the reflection is easy to distinguish. Indeed to reduce this part of the physical process, a grazing angle of incidence is used; this enhances the quantum reflection. This requirement of small incident velocities for the particles means that the non-relativistic approximation to quantum mechanics is all that is required.
Single-dimensional approximation
So far, one usually considers the single-dimensional case of this phenomenon, that is when the potential has translational symmetry in two directions (say  and
and 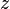 ), such that only a single coordinate (say
), such that only a single coordinate (say  ) is important. In this case one can examine the specular reflection of a slow neutral atom from a solid state surface
.[2][3] Where one has an atom in a region of free space close to a material capable of being polarized, a combination of the pure van der Waals interaction, and the related Casimir-Polder interaction attracts the atom to the surface of the material. The latter force dominates when the atom is comparatively far from the surface, and the former when the atom comes closer to the surface. The intermediate region is controversial as it is dependent upon the specific nature and quantum state of the incident atom.
) is important. In this case one can examine the specular reflection of a slow neutral atom from a solid state surface
.[2][3] Where one has an atom in a region of free space close to a material capable of being polarized, a combination of the pure van der Waals interaction, and the related Casimir-Polder interaction attracts the atom to the surface of the material. The latter force dominates when the atom is comparatively far from the surface, and the former when the atom comes closer to the surface. The intermediate region is controversial as it is dependent upon the specific nature and quantum state of the incident atom.
The condition for a reflection to occur as the atom experiences the attractive potential can be given by the presence of regions of space where the WKB approximation to the atomic wave-function breaks down. If, in accordance with this approximation we write the wavelength of the gross motion of the atom system toward the surface as a quantity local to every region along the  axis,
axis,
where  is the atomic mass,
is the atomic mass, 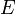 is its energy, and
is its energy, and 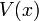 is the potential it experiences, then it is clear that we cannot give meaning to this quantity where,
is the potential it experiences, then it is clear that we cannot give meaning to this quantity where,
That is, in regions of space where the variation of the atomic wavelength is significant over its own length (i.e. the gradient of 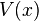 is steep), there is no meaning in the approximation of a local wavelength. This breakdown occurs irrespective of the sign of the potential,
is steep), there is no meaning in the approximation of a local wavelength. This breakdown occurs irrespective of the sign of the potential, 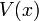 . In such regions part of the incident atom wave-function may become reflected. Such a reflection may occur for slow atoms experiencing the comparatively rapid variation of the van der Waals potential near the material surface. This is just the same kind of phenomenon as occurs when light passes from a material of one refractive index to another of a significantly different index over a small region of space. Irrespective of the sign of the difference in index, there will be a reflected component of the light from the interface. Indeed, quantum reflection from the surface of solid-state wafer allows one to make the quantum optical analogue of a mirror - the atomic mirror - to a high precision.
. In such regions part of the incident atom wave-function may become reflected. Such a reflection may occur for slow atoms experiencing the comparatively rapid variation of the van der Waals potential near the material surface. This is just the same kind of phenomenon as occurs when light passes from a material of one refractive index to another of a significantly different index over a small region of space. Irrespective of the sign of the difference in index, there will be a reflected component of the light from the interface. Indeed, quantum reflection from the surface of solid-state wafer allows one to make the quantum optical analogue of a mirror - the atomic mirror - to a high precision.
Experiments with grazing incidence

Practically, in many experiments with quantum reflection from Si, the grazing incidence angle is used (figure A).
The set-up is mounted in a vacuum chamber to provide a several-meter free path of atoms; the good vacuum (at the level of 10−7 Torr or 130 µPa) is required. The magneto-optical trap (MOT) is used to collect cold atoms, usually excited He or Ne, approaching the point-like source of atoms. The excitation of atoms is not essential for the quantum reflection but it allows the efficient trapping and cooling using optical frequencies. In addition, the excitation of atoms allows the registration at the micro-channel plate (MCP) detector (bottom of the figure). Movable edges are used to stop atoms which do not go toward the sample (for example a Si plate), providing the collimated atomic beam. The He-Ne laser was used to control the orientation of the sample and measure the grazing angle 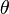 . At the MCP, there was observed relatively intensive strip of atoms which come straightly (without reflection) from the MOT, by-passing the sample, strong shadow of the sample (the thickness of this shadow could be used for rough control of the grazing angle), and the relatively weak strip produced by the reflected atoms. The ratio
. At the MCP, there was observed relatively intensive strip of atoms which come straightly (without reflection) from the MOT, by-passing the sample, strong shadow of the sample (the thickness of this shadow could be used for rough control of the grazing angle), and the relatively weak strip produced by the reflected atoms. The ratio  of density of atoms registered at the center of this strip to the density of atoms at the directly illuminated region was considered as efficiency of quantum reflection, i.e., reflectivity. This reflectivity strongly depends on the grazing angle and speed of atoms.
of density of atoms registered at the center of this strip to the density of atoms at the directly illuminated region was considered as efficiency of quantum reflection, i.e., reflectivity. This reflectivity strongly depends on the grazing angle and speed of atoms.
In the experiments with Ne atoms, usually just fall down, when the MOT is suddenly switched off. Then, the speed of atoms is determined as 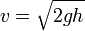 , where
, where 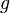 is acceleration of free fall, and
is acceleration of free fall, and 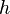 is distance from the MOT to the sample. In experiments described, this distance was of order of 0.5 meters (2 ft), providing the speed of order of 3 m/s (6.7 mph; 11 km/h). Then, the transversal wavenumber can be calculated as
is distance from the MOT to the sample. In experiments described, this distance was of order of 0.5 meters (2 ft), providing the speed of order of 3 m/s (6.7 mph; 11 km/h). Then, the transversal wavenumber can be calculated as 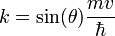 , where
, where 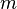 is mass of the atom, and
is mass of the atom, and 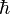 is the Planck constant.
is the Planck constant.
In the case with He, the additional resonant laser could be used to release the atoms and provide them an additional velocity; the delay since the release of the atoms till the registration allowed to estimate this additional velocity; roughly, 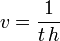 , where
, where 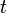 is time delay since the release of atoms till the click at the detector. Practically,
is time delay since the release of atoms till the click at the detector. Practically,  could vary from 20 to 130 m/s (45 to 291 mph; 72 to 468 km/h).[4][5][6]
could vary from 20 to 130 m/s (45 to 291 mph; 72 to 468 km/h).[4][5][6]
Although the scheme at the figure looks simple, the extend facility is necessary to slow atoms, trap them and cool to millikelvin temperature, providing a micrometre size source of cold atoms. Practically, the mounting and maintaining of this facility (not shown in the figure) is the heaviest job in the experiments with quantum reflection of cold atoms. The possibility of an experiment with the quantum reflection with just a pinhole instead of MOT are discussed in the literature.[6]
Casimir and van der Waals attraction
Despite this, there is some doubt as to the physical origin of quantum reflection from solid surfaces. As was briefly mentioned above, the potential in the intermediate region between the regions dominated by the Casimir-Polder and Van der Waals interactions requires an explicit Quantum Electrodynamical calculation for the particular state and type of atom incident on the surface. Such a calculation is very difficult. Indeed, there is no reason to suppose that this potential is solely attractive within the intermediate region. Thus the reflection could simply be explained by a repulsive force, which would make the phenomenon not quite so surprising. Furthermore, a similar dependence for reflectivity on the incident velocity is observed in the case of the adsorption of particles in vicinity of a surface. In the simplest case, such absorption could be described with a non-Hermitian potential (i.e. one where probability is not conserved). Until 2006, the published papers interpreted the reflection in terms of a Hermitian potential
this assumption allows to build a quantitative theory .[8]
Efficient quantum reflection

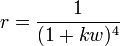 , compared to experimental data.
, compared to experimental data.A qualitative estimate for the efficiency of quantum reflection can be made using dimensional analysis. Letting  be mass of the atom and
be mass of the atom and 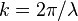 the normal component of its wave-vector, then the energy of the normal motion of the particle,
the normal component of its wave-vector, then the energy of the normal motion of the particle,
should be compared to the potential, 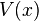 of interaction. The distance,
of interaction. The distance, 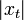 at which
at which 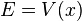 can be considered as the distance the which the atom will come across a troublesome discontinuity in the potential. This is the point at which the WKB method truly becomes nonsense. The condition for efficient quantum reflection can be written as
can be considered as the distance the which the atom will come across a troublesome discontinuity in the potential. This is the point at which the WKB method truly becomes nonsense. The condition for efficient quantum reflection can be written as 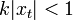 . In other words the wavelength is small compared to the distance at which the atom may become reflected from the surface. If this condition holds, the aforementioned effect of the discrete character of the surface may be neglected. This argument produces a simple estimate for the reflectivity,
. In other words the wavelength is small compared to the distance at which the atom may become reflected from the surface. If this condition holds, the aforementioned effect of the discrete character of the surface may be neglected. This argument produces a simple estimate for the reflectivity,  ,
,
which shows good agreement with experimental data for excited neon and helium atoms, reflected from a flat silicon surface (fig.1), see [6] and references therein. Such a fit is also in good agreement with a single-dimensional analysis of the scattering of atoms from an attractive potential,.[9] Such agreement indicates, that, at least in the case of noble gases and Si surface, the quantun reflection can be described with single-dimensional hermitian potential, as the result of attraction of atoms to the surface.
Ridged mirror
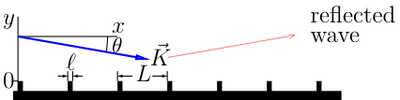
The effect of quantum reflection can be enhanced using ridged mirrors
.[10] If one produces a surface consisting of a set of narrow ridges then the resulting non-uniformity of the material allows the reduction of the effective van der Waals constant; this extends the working ranges of the grazing angle. For this reduction to be valid, we must have small distances,  between the ridges. Where
between the ridges. Where  becomes large, the non-uniformity is such that the ridged mirror must be interpreted in terms of multiple Fresnel diffraction [4] or the Zeno effect;[5] these interpretations give similar estimates for the reflectivity
.[11] See ridged mirror for the details.
becomes large, the non-uniformity is such that the ridged mirror must be interpreted in terms of multiple Fresnel diffraction [4] or the Zeno effect;[5] these interpretations give similar estimates for the reflectivity
.[11] See ridged mirror for the details.
Similar enhancement of quantum reflection takes place where one has particles incident on an array of pillars .[12] This was observed with very slow atoms (Bose–Einstein condensate) at almost normal incidence.
Application of quantum reflection
Quantum reflection makes the idea of solid-state atomic mirrors and atomic-beam imaging systems (atomic nanoscope) possible.[6] The use of quantum reflection in the production of atomic traps has also been suggested.[9] Up to year 2007, no commercial application of quantum reflection was reported.
References
- ↑ Quantum Reflection, workshop; October 22–24, 2007, Cambridge, Massachusetts, USA; http://cfa-www.harvard.edu/itamp/QuantumReflection.html
- ↑ F.Shimizu (2001). "Specular Reflection of Very Slow Metastable Neon Atoms from a Solid Surface". Physical Review Letters 86 (6): 987–990. Bibcode:2001PhRvL..86..987S. doi:10.1103/PhysRevLett.86.987. PMID 11177991.
- ↑ H.Oberst; Y.Tashiro, K.Shimizu, F.Shimizu (2005). "Quantum reflection of He* on silicon". Physical Review A 71 (5): 052901. Bibcode:2005PhRvA..71e2901O. doi:10.1103/PhysRevA.71.052901.
- ↑ 4.0 4.1 H.Oberst; D.Kouznetsov, K.Shimizu, J.Fujita, and F.Shimizu (2005). "Fresnel Diffraction Mirror for an Atomic Wave". Physical Review Letters 94: 013203. Bibcode:2005PhRvL..94a3203O. doi:10.1103/PhysRevLett.94.013203.
- ↑ 5.0 5.1 D.Kouznetsov; H.Oberst (2005). "Reflection of Waves from a Ridged Surface and the Zeno Effect". Optical Review 12 (5): 1605–1623. Bibcode:2005OptRv..12..363K. doi:10.1007/s10043-005-0363-9.
- ↑ 6.0 6.1 6.2 6.3 D.Kouznetsov; H.Oberst, K.Shimizu, A.Neumann, Y.Kuznetsova, J.-F.Bisson, K.Ueda, S.R.J.Brueck (2006). "Ridged atomic mirrors and atomic nanoscope". Journal of Physics B 39 (7): 1605–1623. Bibcode:2006JPhB...39.1605K. doi:10.1088/0953-4075/39/7/005.
- ↑ H.Friedrich; G.Jacoby, C.G.Meister (2002). "quantum reflection by Casimir–van der Waals potential tails". Physical Review A 65 (3): 032902. Bibcode:2002PhRvA..65c2902F. doi:10.1103/PhysRevA.65.032902.
- ↑ F.Arnecke; H.Friedrich, J.Madroñero (2006). "Effective-range theory for quantum reflection amplitudes". Physical Review A 74 (6): 062702. Bibcode:2006PhRvA..74f2702A. doi:10.1103/PhysRevA.74.062702.
- ↑ 9.0 9.1 J.Madroñero; H.Friedrich (2007). "Influence of realistic atom wall potentials in quantum reflection traps". Physical Review A 75 (2): 022902. Bibcode:2007PhRvA..75b2902M. doi:10.1103/PhysRevA.75.022902.
- ↑ F.Shimizu; J. Fujita (2002). "Giant Quantum Reflection of Neon Atoms from a Ridged Silicon Surface". Journal of the Physical Society of Japan 71: 5–8. arXiv:physics/0111115. Bibcode:2002JPSJ...71....5S. doi:10.1143/JPSJ.71.5.
- ↑ D.Kouznetsov; H.Oberst (2005). "Scattering of waves at ridged mirrors" (PDF). Physical Review A 72: 013617. Bibcode:2005PhRvA..72a3617K. doi:10.1103/PhysRevA.72.013617.
- ↑ T.A.Pasquini; M.Saba, G.-B.Jo, Y.Shin, W.Ketterle, D.E.Pritchard, T.A.Savas, N. Mulders. (2006). "Low Velocity Quantum Reflection of Bose-Einstein Condensate". Physical Review Letters 97 (9): 093201. arXiv:cond-mat/0603463. Bibcode:2006PhRvL..97i3201P. doi:10.1103/PhysRevLett.97.093201.
See also
- Atom optics
- Ridged mirror
- Casimir force
- van der Waals potential