Quantum paraelectricity
Quantum paraelectricity[1] is a type of incipient ferroelectricity where the onset of ferroelectric order is suppressed by quantum fluctuations.[2] From the soft mode theory of ferroelectricity,[3] this occurs when a ferroelectric instability is stabilized by quantum fluctuations. In this case the soft-mode frequency never becomes unstable (Fig. 1a) as opposed to a regular ferroelectric.
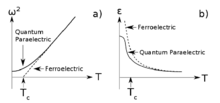
Experimentally this is associated with an anomalous behaviour of the dielectric susceptibility, for example in SrTiO3.[4] In a normal ferroelectric, close to the onset of the phase transition the dielectric susceptibility diverges as the temperature approaches the Curie temperature. However, in the case of a quantum paraelectric the dielectric susceptibility diverges until it reaches a temperature low enough for quantum effects to cancel out the ferroelectricity (Fig. 1b). In the case of SrTiO3 this is around 4K.
Other known quantum paraelectrics are KTaO3 and potentially CaTiO3.[5]
References
- ↑ See R. A. Cowley (1963). "Lattice Dynamics and Phase Transitions of Strontium Titanate". Physical Review 134 (4A): A981. Bibcode:1964PhRv..134..981C. doi:10.1103/PhysRev.134.A981.
- ↑ See T. Schneider, H. Beck, and E. Stoll (1976). "Quantum effects in an n-component vector model for structural phase transitions". Physical Review B 13 (3): 1123. Bibcode:1976PhRvB..13.1123S. doi:10.1103/PhysRevB.13.1123.
- ↑ See W. Cochran (1960). "Crystal stability and the theory of ferroelectricity". Advances in Physics 9 (36): 387. Bibcode:1960AdPhy...9..387C. doi:10.1080/00018736000101229.
- ↑ See K. A. Muller and H. Burkhard (1979). "SrTiO3: An intrinsic quantum paraelectric below 4K". Physical Review B 19 (7): 3593. Bibcode:1979PhRvB..19.3593M. doi:10.1103/PhysRevB.19.3593.
- ↑ See D. Rytz and U. T. Höchli and H. Bilz (1980). "Dielectric susceptibility in quantum ferroelectrics". Physical Review B 22: 359. Bibcode:1980PhRvB..22..359R. doi:10.1103/PhysRevB.22.359.