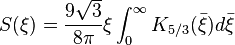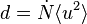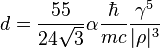Quantum excitation (accelerator physics)

Quantum excitation is the effect in circular accelerators or storage rings whereby the discreteness of photon emission causes the charged particles (typically electrons) to undergo a random walk or diffusion process.

Mechanism

An electron moving through a magnetic field emits radiation. One can compute the expected amount of radiation by computing the classical power. Considering quantum mechanics, however, one finds that this radiation is emitted in discrete packets of photons. For this description, one should determine the distribution of number of emitted photons and also the energy spectrum for the electron.

In particular, the spectrum of a bending magnet is given by

S(\xi)=\frac{9\sqrt{3}}{8\pi}\xi\int_0^\infty K_{5/3}(\bar \xi) d\bar \xi

The diffusion coefficient is given by

d= \dot N\langle u^2\rangle

The result of this calculation is

d= \frac{55}{24\sqrt{3}}\alpha \frac{\hbar}{mc}\frac{\gamma^5}{|\rho|^3}

Further reading

For an early analysis of the effect of quantum excitation on electron beam dynamics in storage rings, see the article by Matt Sands.[1]

References

  1. ↑ http://www.slac.stanford.edu/pubs/slacreports/slac-r-121.html The Physics of Electron Storage Rings: An Introduction by Matt Sands