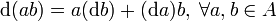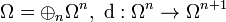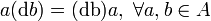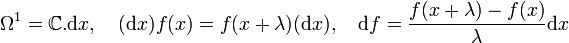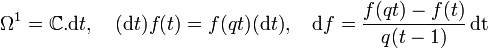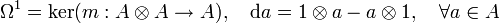Quantum differential calculus

In quantum geometry or noncommutative geometry a quantum differential calculus or noncommutative differential structure on an algebra $A$ over a field $k$ means the specification of a space of differential forms over the algebra. The algebra $A$ here is regarded as a coordinate ring but it is important that it may be noncommutative and hence not an actual algebra of coordinate functions on any actual space, so this represents a point of view replacing the specification for an actual space of a differentiable structure. In ordinary differential geometry one can multiply differential 1-forms by functions form the left and the right and has an exterior derivative. Correspondingly, a first order quantum differential calculus means at least the following:

1. An $A$ - $A$ -bimodule $\Omega^1$ over $A$ , i.e. one can multiply elements of $\Omega^1$ by elements of $A$ in an associative way:

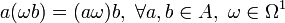a(\omega b)=(a\omega)b,\ \forall a,b\in A,\ \omega\in\Omega^1

2. A linear map 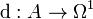${\rm d}:A\to\Omega^1$ obeying the Leibniz rule

{\rm d}(ab)=a({\rm d}b)+({\rm d}a)b,\ \forall a,b\in A

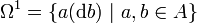
3. $\Omega^1=\{a({\rm d}b)\ |\ a,b\in A\}$

4. (optional connectedness condition) 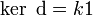$\ker\ {\rm d}=k1$

The last condition is not always imposed but holds in ordinary geometry when the manifold is connected. It says that the only functions killed by 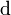${\rm d}$ are constant functions.

An exterior algebra or differential graded algebra structure over $A$ means a compatible extension of $\Omega^1$ to include analogues of higher order differential forms

\Omega=\oplus_n\Omega^n,\ {\rm d}:\Omega^n\to\Omega^{n+1}

obeying a graded-Leibniz rule with respect to an associative product on 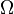$\Omega$ and obeying 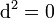${\rm d}^2=0$ . Here 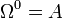$\Omega^0=A$ and it is usually required that 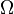$\Omega$ is generated by 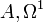$A,\Omega^1$ . The product of differential forms is called the exterior or wedge product and often denoted 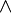$\wedge$ . The noncommutative or quantum de Rham cohomology is defined as the cohomology of this complex.

A higher order differential calculus can mean an exterior algebra or it can mean the partial specification of one up to some highest degree and with products that would result in a degree beyond the highest being unspecified.

The above definition lies at the crossroads of two approaches to noncommutative geometry. In the Connes approach a more fundamental object is a replacement for the Dirac operator in the form of a spectral triple, and an exterior algebra can be constructed from this data. In the quantum groups approach to noncommutative geometry one starts with the algebra and a choice of first order calculus but constrained by covariance under a quantum group symmetry.

Note

The above definition is minimal and gives something more general than classical differential calculus even when the algebra $A$ is commutative or functions on an actual space. This is because we do not demand that

a({\rm d}b)=({\rm db})a,\ \forall a,b\in A

since this would imply that 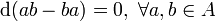${\rm d}(ab-ba)=0,\ \forall a,b\in A$ , which would violate axiom 4 when the algebra was noncommutative. As a byproduct, this enlarged definition includes finite difference calculi and quantum differential calculi on finite sets and finite groups (finite group Lie algebra theory).

Examples

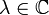1. For $A={\Bbb C}[x]$ the algebra of polynomials in one variable the translation-covariant quantum differential calculi are parametrized by $\lambda\in \Bbb C$ and take the form

\Omega^1={\Bbb C}.{\rm d}x,\quad ({\rm d}x)f(x)=f(x+\lambda)({\rm d}x),\quad {\rm d}f={f(x+\lambda)-f(x)\over\lambda}{\rm d}x

This shows how finite differences arise naturally in quantum geometry. Only the limit 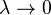$\lambda\to 0$ has functions commuting with 1-forms, which is the special case of high school differential calculus.

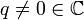2. For $A={\Bbb C}[t,t^{-1}]$ the algebra of functions on an algebraic circle, the translation (i.e. circle-rotation)-covariant differential calculi are parametrized by $q\ne 0\in \Bbb C$ and take the form

\Omega^1={\Bbb C}.{\rm d}t,\quad ({\rm d}t)f(t)=f(qt)({\rm d}t),\quad {\rm d}f={f(qt)-f(t)\over q(t-1)}\,{\rm dt}

This shows how $q$ -differentials arise naturally in quantum geometry.

3. For any algebra $A$ one has a universal differential calculus defined by

\Omega^1=\ker(m:A\otimes A\to A),\quad {\rm d}a=1\otimes a-a\otimes 1,\quad\forall a\in A

where $m$ is the algebra product. By axiom 3., any first order calculus is a quotient of this.

Quantum differential calculus

Note

Examples

See also

Further reading