Quantitative susceptibility mapping

A volume rendered brain QSM acquired at 3 Teslas and reconstructed with Morphology Enabled Dipole Inversion (MEDI).

Quantitative Susceptibility Mapping (QSM) provides a novel contrast mechanism in Magnetic Resonance Imaging (MRI) different from traditional Susceptibility Weighted Imaging.[1][2][3][4] The voxel intensity in QSM is linearly proportional to the underlying tissue apparent magnetic susceptibility, which is useful for chemical identification and quantification of specific biomarkers including iron, calcium, gadolinium, and super paramagnetic iron oxide (SPIO) nano-particles. QSM utilizes phase images, solves the magnetic field to susceptibility source inverse problem, and generates a three-dimensional susceptibility distribution. Due to its quantitative nature and sensitivity to certain kinds of material, potential QSM applications include standardized quantitative stratification of cerebral microbleeds and neurodegenerative disease, accurate gadolinium quantification in contrast enhanced MRI, and direct monitoring of targeted theranostic drug biodistribution in nanomedicine.

Background

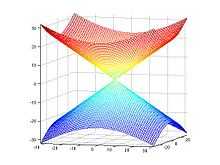
A visualization of the cone in Fourier domain.

In MRI, the local field 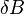\delta B induced by non-ferromagnetic biomaterial susceptibility along the main polarization B₀ field is the convolution of the volume susceptibility distribution 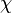\chi with the dipole kernel 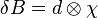d: \delta B = d \otimes \chi. This spatial convolution can be expressed as a point-wise multiplication in Fourier domain:[5][6] 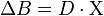\Delta B = D \cdot \Chi. This Fourier expression provides an efficient way to predict the field perturbation when the susceptibility distribution is known. However, the field to source inverse problem involves division by zero at a pair of cone surfaces at the magic angle with respect to B₀ in the Fourier domain. Consequently, susceptibility is underdetermined at the spatial frequencies on the cone surface, which often leads to severe streaking artifacts in the reconstructed QSM.

Techniques

Data acquisition

In principle, any 3D gradient echo sequence can be used for data acquisition. In practice, high resolution imaging with a moderately long echo time is preferred to obtain sufficient susceptibility effects, although the optimal imaging parameters depend on the specific applications and the field strength. A multi-echo acquisition is beneficial for accurate B₀ field measurement without the contribution from B1 inhomogeneity. Flow compensation may further improve the accuracy of susceptibility measurement in venous blood, but there are certain technical difficulties to devise a fully flow compensated multi-echo sequence.

Background field removal

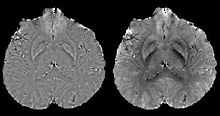
Estimated local field maps using Left) high-pass filtering method, Right) Projection onto Dipole Fields (PDF) method.

In human brain quantitative susceptibility mapping, only the local susceptibility sources inside the brain are of interest. However, the magnetic field induced by the local sources is inevitably contaminated by the field induced by other sources such as main field inhomogeneity (imperfect shimming) and the air-tissue interface, whose susceptibility difference is orders of magnitudes stronger than that of the local sources. Therefore, the non-biological background field needs to be removed for clear visualization on phase images and precise quantification on QSM.

Ideally, the background field can be directly measured with a separate reference scan, where the sample of interest is replaced by a uniform phantom with the same shape while keeping the scanner shimming identical. However, for clinical application, such an approach is impossible and post-processing based methods are preferred. Traditional heuristic methods, including high-pass filtering, are useful for the background field removal, although they also tamper with the local field and degrade the quantitative accuracy.

More recent background field removal methods directly or indirectly exploit the fact that the background field is a harmonic function. Two recent methods which are based on physical principles, Projection onto Dipole Fields (PDF)[7] and Sophisticated Harmonic Artifact Reduction on Phase data (SHARP),[8] demonstrated improved contrast and higher precision on the estimated local field. Both methods model the background field as a magnetic field generated by an unknown background susceptibility distribution, and differentiate it from the local field using either the approximate orthogonality or the harmonic property. The background field can also be directly computed by solving the Laplace's equation with simplified boundary values, as demonstrated in the Laplacian boundary value (LBV) method.[9]

Field-to-source inversion

The field-to-source inverse problem can be solved by several methods with various associated advantages and limitations.

Calculation Of Susceptibility through Multiple Orientation Sampling (COSMOS)[10][11]

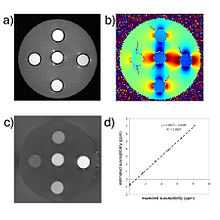
The first QSM image reconstructed using COSMOS to quantify gadolinium concentrations in vials. a)magnitude image; b)field map; c)QSM; d)linear regression.

COSMOS solves the inverse problem by oversampling from multiple orientations.[10] COSMOS utilizes the fact that the zero cone surface in the Fourier domain is fixed at the magic angle with respect to the B₀ field. Therefore, if an object is rotated with respect to the B₀ field, then in the object's frame, the B₀ field is rotated and thus the cone. Consequently, data that cannot be calculated due to the cone becomes available at the new orientations.

COSMOS assumes a model-free susceptibility distribution and keeps full fidelity to the measured data. This method has been validated extensively in in vitro, ex vivo and phantom experiments. Quantitative susceptibility maps obtained from in vivo human brain imaging also showed high degree of agreement with previous knowledge about brain anatomy. Three orientations are generally required for COSMOS, limiting the practicality for clinical applications. However, it may serve as a reference standard when available for calibrating other techniques.

Morphology Enabled Dipole Inversion (MEDI)[12]

A unique advantage of MRI is that it provides not only the phase image but also the magnitude image. In principle, the contrast change, or equivalently the edge, on a magnitude image arises from the underlying change of tissue type, which is the same cause for the change of susceptibility. This observation is translated into mathematics in MEDI, where edges in a QSM which do not exist in the corresponding magnitude image are sparsified by solving a weighted 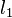l_1 norm minimization problem.[13]

MEDI has also been validated extensively in phantom, in vitro and ex vivo experiments. In in vivo human brain, MEDI calculated QSM showed similar results compared to COSMOS without statistically significant difference.[14] MEDI only requires a single angle acquisition, so it is a more practical solution to QSM.

Thresholded K-space Division (TKD)[11][15]

The underdetermined data in Fourier domain is only at the location of the cone and its immediate vicinity. For this region in k-space, spatial-frequencies of the dipole kernel are set to a predetermined non-zero value for the division. Investigation of more advanced strategies for recovering data in this k-space region is also a topic of ongoing research.[16]

Thresholded k-space division only requires a single angle acquisition, and benefits from the ease of implementation as well as the fast calculation speed. However, streaking artifacts are frequently present in the QSM and the susceptibility value is underestimated compared to COSMOS calculated QSM.

Potential clinical applications

Differentiating calcification from iron

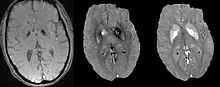
Differentiation between calcification and iron. From left to right are magnitude, phase and QSM.

It has been confirmed in in vivo and phantom experiments that cortical bones, whose major composition is calcification, are diamagnetic compared to water.[10][17] Therefore, it is possible to use this diamagnetism to differentiate calcifications from iron deposits that usually demonstrate strong paramagnetism.[18] This may allow QSM to serve as a problem solving tool for the diagnosis of confounding hypointense findings on T2* weighted images.

Quantification of contrast agent

For exogenous susceptibility sources, the susceptibility value is theoretically linearly proportional to the concentration of the contrast agent. This provides a new way for in vivo quantification of gadolinium or SPIO concentrations.[19]

References

  1. ↑ 1st International Workshop on MRI Phase Contrast and Quantitative Susceptibility Mapping, Jena (2011)
  2. ↑ 2nd International Workshop on MRI Phase Contrast & Quantitative Susceptibility Mapping, Cornell (2013)
  3. ↑ 3rd International Workshop on MRI Phase Contrast & Quantitative Susceptibility Mapping, Duke (2014)
  4. ↑ Y. Wang and T. Liu, Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker, MRM 73, 82-101, (2015)
  5. ↑ Salomir, Rares; De Senneville, Baudouin Denis; Moonen, Chrit TW (2003). "A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility". Concepts in Magnetic Resonance 19B: 26–34. doi:10.1002/cmr.b.10083.
  6. ↑ Marques, J.P.; Bowtell, R. (2005). "Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility". Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering 25B: 65–78. doi:10.1002/cmr.b.20034.
  7. ↑ Liu, Tian; Khalidov, Ildar; de Rochefort, Ludovic; Spincemaille, Pascal et al. (2011). "A novel background field removal method for MRI using projection onto dipole fields". NMR in Biomedicine 24 (9): 1129–36. doi:10.1002/nbm.1670. PMID 21387445.
  8. ↑ Schweser, Ferdinand; Deistung, Andreas; Lehr, Berengar Wendel; Reichenbach, Jürgen Rainer (2011). "Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism?". NeuroImage 54 (4): 2789–2807. doi:10.1016/j.neuroimage.2010.10.070. PMID 21040794.
  9. ↑ Zhou, Dong; Liu, Tian; Spincemaille, Pascal; Wang, Yi (2014). "Background field removal by solving the Laplacian boundary value problem". NMR in Biomedicine 27: 312–9. doi:10.1002/nbm.3064.
  10. ↑ 10.0 10.1 10.2 Liu, Tian; Spincemaille, Pascal; De Rochefort, Ludovic; Kressler, Bryan et al. (2009). "Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI". Magnetic Resonance in Medicine 61 (1): 196–204. doi:10.1002/mrm.21828. PMID 19097205.
  11. ↑ 11.0 11.1 Wharton, Sam; Schäfer, Andreas; Bowtell, Richard (2010). "Susceptibility mapping in the human brain using threshold-based k-space division". Magnetic Resonance in Medicine 63 (5): 1292–304. doi:10.1002/mrm.22334. PMID 20432300.
  12. ↑ De Rochefort, Ludovic; Liu, Tian; Kressler, Bryan; Liu, Jing et al. (2009). "Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: Validation and application to brain imaging". Magnetic Resonance in Medicine: 194–206. doi:10.1002/mrm.22187.
  13. ↑ http://cds.ismrm.org/protected/10MProceedings/files/4996_705.PDF Liu J, Liu T, de Rochefort L, Khalidov I, Prince M, Wang Y. 2010 Quantitative susceptibility mapping by regulating the field to source inverse problem with a sparse prior derived from the Maxwell Equation: validation and application to brain Proc. Intl. Soc. Mag. Reson. Med. 18 (2010):4996.
  14. ↑ Liu, Tian; Liu, Jing; de Rochefort, Ludovic; Spincemaille, Pascal et al. (September 2011). "Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: Comparison with COSMOS in human brain imaging". Magnetic Resonance in Medicine 66 (3): 777–83. doi:10.1002/mrm.22816. PMID 21465541.
  15. ↑ Shmueli, Karin; De Zwart, Jacco A.; Van Gelderen, Peter; Li, Tie-Qiang et al. (2009). "Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data". Magnetic Resonance in Medicine 62 (6): 1510–22. doi:10.1002/mrm.22135. PMID 19859937.
  16. ↑ Li, Wei; Wu, Bing; Liu, Chunlei (2011). "Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition". NeuroImage 55 (4): 1645–56. doi:10.1016/j.neuroimage.2010.11.088. PMC 3062654. PMID 21224002.
  17. ↑ De Rochefort, Ludovic; Brown, Ryan; Prince, Martin R.; Wang, Yi (2008). "Quantitative MR susceptibility mapping using piece-wise constant regularized inversion of the magnetic field". Magnetic Resonance in Medicine 60 (4): 1003–9. doi:10.1002/mrm.21710. PMID 18816834.
  18. ↑ Schweser, Ferdinand; Deistung, Andreas; Lehr, Berengar W.; Reichenbach, JüRgen R. (2010). "Differentiation between diamagnetic and paramagnetic cerebral lesions based on magnetic susceptibility mapping". Medical Physics 37 (10): 5165–78. doi:10.1118/1.3481505. PMID 21089750.
  19. ↑ De Rochefort, Ludovic; Nguyen, Thanh; Brown, Ryan; Spincemaille, Pascal et al. (2008). "In vivo quantification of contrast agent concentration using the induced magnetic field for time-resolved arterial input function measurement with MRI". Medical Physics 35 (12): 5328–39. doi:10.1118/1.3002309. PMID 19175092.