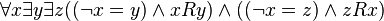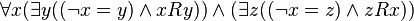Quantifier rank
In mathematical logic, the quantifier rank of a formula is the depth of nesting of its quantifiers. It plays an essential role in model theory.
Notice that the quantifier rank is a property of the formula itself (i.e. the expression in a language). Thus two logically equivalent formulae can have different quantifier ranks, when they express the same thing in different ways.
Definition
Quantifier Rank of a Formula in First-order language (FO)
Let φ be a FO formula. The quantifier rank of φ, written qr(φ), is defined as
-
 , if φ is atomic.
, if φ is atomic. -
 .
. -
 .
. -
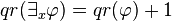 .
.
Remarks
- We write FO[n] for the set of all first-order formulas φ with
 .
. - Relational FO[n] (without function symbols) is always of finite size, i.e. contains a finite number of formulas
- Notice that in Prenex normal form the Quantifier Rank of φ is exactly the number of quantifiers appearing in φ.
Quantifier Rank of a higher order Formula
- For Fixpoint logic, with a least fix point operator LFP:
- qr([LFPφ]y) = 1 + qr( φ)
...
Examples
- A sentence of quantifier rank 2:
- ∀x∃y R(x, y)
- A formula of quantifier rank 1:
- ∀x R(y, x) ∧ ∃x R(x, y)
- A formula of quantifier rank 0:
- R(x, y) ∧ x ≠ y
- A formula in prenex normal form of quantifier rank 3:
- A formula, equivalent to the latter, although of quantifier rank 2:
See also
- Prenex normal form
- Ehrenfeucht game
- Quantifier
References
- Ebbinghaus, Heinz-Dieter; Flum, Jörg (1995), Finite Model Theory, Springer, ISBN 978-3-540-60149-4.
- Grädel, Erich; Kolaitis, Phokion G.; Libkin, Leonid; Maarten, Marx; Spencer, Joel; Vardi, Moshe Y.; Venema, Yde; Weinstein, Scott (2007), Finite model theory and its applications, Texts in Theoretical Computer Science. An EATCS Series, Berlin: Springer-Verlag, p. 133, ISBN 978-3-540-00428-8, Zbl 1133.03001.
External links
- Quantifier Rank Spectrum of L-infinity-omega BA Thesis, 2000