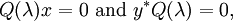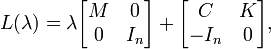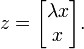Quadratic eigenvalue problem
In mathematics, the quadratic eigenvalue problem[1] (QEP), is to find scalar eigenvalues 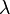 , left eigenvectors
, left eigenvectors 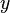 and right eigenvectors
and right eigenvectors 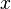 such that
such that
where 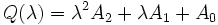 , with matrix coefficients
, with matrix coefficients 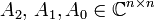 and we require that
and we require that 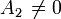 , (so that we have a nonzero leading coefficient). There are
, (so that we have a nonzero leading coefficient). There are 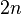 eigenvalues that may be infinite or finite, and possibly zero. This is a special case of a nonlinear eigenproblem.
eigenvalues that may be infinite or finite, and possibly zero. This is a special case of a nonlinear eigenproblem. 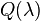 is also known as a quadratic matrix polynomial.
is also known as a quadratic matrix polynomial.
Applications
A QEP can result in part of the dynamic analysis of structures discretized by the finite element method. In this case the quadratic, 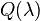 has the form
has the form 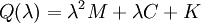 , where
, where 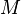 is the mass matrix,
is the mass matrix, 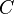 is the damping matrix and
is the damping matrix and 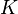 is the stiffness matrix.
Other applications include vibro-acoustics and fluid dynamics.
is the stiffness matrix.
Other applications include vibro-acoustics and fluid dynamics.
Methods of solution
Direct methods for solving the standard or generalized eigenvalue problems 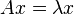 and
and 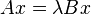 are based on transforming the problem to Schur or Generalized Schur form. However, there is no analogous form for quadratic matrix polynomials.
One approach is to transform the quadratic matrix polynomial to a linear matrix pencil (
are based on transforming the problem to Schur or Generalized Schur form. However, there is no analogous form for quadratic matrix polynomials.
One approach is to transform the quadratic matrix polynomial to a linear matrix pencil (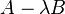 ), and solve a generalized
eigenvalue problem. Once eigenvalues and eigenvectors of the linear problem have been determined, eigenvectors and eigenvalues of the quadratic can be determined.
), and solve a generalized
eigenvalue problem. Once eigenvalues and eigenvectors of the linear problem have been determined, eigenvectors and eigenvalues of the quadratic can be determined.
The most common linearization is the first companion linearization
where 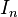 is the
is the  -by-
-by- identity matrix, with corresponding eigenvector
identity matrix, with corresponding eigenvector
We solve 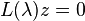 for
for  and
and 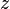 , for example by computing the Generalized Schur form. We can then
take the first
, for example by computing the Generalized Schur form. We can then
take the first  components of
components of 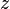 as the eigenvector
as the eigenvector  of the original quadratic
of the original quadratic 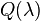 .
.
References
- ↑ F. Tisseur and K. Meerbergen, The quadratic eigenvalue problem, SIAM Rev., 43 (2001), pp. 235–286.