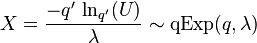q-exponential distribution
|
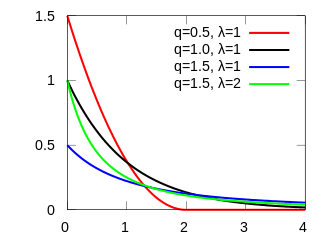
Probability density function
| |
| Parameters |
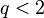 shape (real) shape (real) 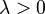 rate (real) rate (real) |
|---|---|
| Support |
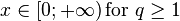 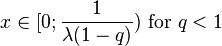 |
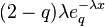 | |
| CDF |
 |
| Mean |
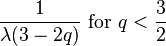 Otherwise undefined |
| Median |
 |
| Mode | 0 |
| Variance |
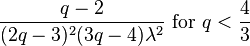 |
| Skewness |
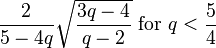 |
| Ex. kurtosis |
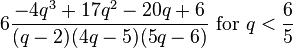 |
The q-exponential distribution is a probability distribution arising from the maximization of the Tsallis entropy under appropriate constraints, including constraining the domain to be positive. It is one example of a Tsallis distribution. The q-exponential is a generalization of the exponential distribution in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon Entropy.[1] The exponential distribution is recovered as 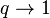 .
.
Characterization
Probability density function
The q-exponential distribution has the probability density function
where
is the q-exponential, if q≠1. When q=1, eq(x) is just exp(x).
Derivation
In a similar procedure to how the exponential distribution can be derived using the standard Boltzmann–Gibbs entropy or Shannon entropy and constraining the domain of the variable to be positive, the q-exponential distribution can be derived from a maximization of the Tsallis Entropy subject to the appropriate constraints.
Relationship to other distributions
The q-exponential is a special case of the Generalized Pareto distribution where
The q-exponential is the generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support. The Lomax parameters are:
As the Lomax distribution is a shifted version of the Pareto distribution, the q-exponential is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:
Generating random deviates
Random deviates can be drawn using Inverse transform sampling. Given a variable U that is uniformly distributed on the interval (0,1), then
where 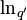 is the q-logarithm and
is the q-logarithm and 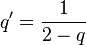
Applications
Economics (econophysics)
The q-exponential distribution has been used to describe the distribution of wealth (assets) between individuals.[2]
See also
Notes
- ↑ Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics-an overview after 20 years. Braz. J. Phys. 2009, 39, 337–356
- ↑ Adrian A. Dragulescu Applications of physics to economics and finance: Money, income, wealth, and the stock market arXiv:cond-mat/0307341v2
Further reading
- Juniper, J. (2007) "The Tsallis Distribution and Generalised Entropy: Prospects for Future Research into Decision-Making under Uncertainty", Centre of Full Employment and Equity, The University of Newcastle, Australia
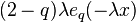
![e_q(x) = [1+(1-q)x]^{1 \over 1-q}](../I/m/d8708c16e1cf6c2a79fd3d0e7b7464c8.png)
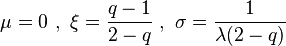
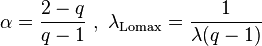
![\text{If } X \sim \mathrm{qExp}(q,\lambda) \text{ and } Y \sim \left[\text{Pareto}
\left(
x_m = {1 \over {\lambda (q-1)}}, \alpha = { {2-q} \over {q-1}}
\right) -x_m
\right],
\text{ then } X \sim Y \,](../I/m/ad0f09142260ce67b63b3d532f8369af.png)