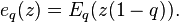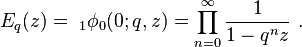q-exponential
Not to be confused with the Tsallis q-exponential.
In combinatorial mathematics, the q-exponential is a q-analog of the exponential function, namely the eigenfunction of the q-derivative
Definition
The q-exponential 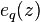 is defined as
is defined as
where ![[n]_q!](../I/m/4068da6f34e0edc79705024cdc294e3d.png) is the q-factorial and
is the q-factorial and
is the q-Pochhammer symbol. That this is the q-analog of the exponential follows from the property
where the derivative on the left is the q-derivative. The above is easily verified by considering the q-derivative of the monomial
Here, ![[n]_q](../I/m/94afffce1a5ca1d85aca3a7ed181aa2f.png) is the q-bracket.
is the q-bracket.
Properties
For real  , the function
, the function 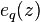 is an entire function of z. For
is an entire function of z. For 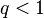 ,
, 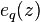 is regular in the disk
is regular in the disk 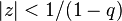 .
.
Note the inverse, 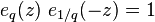 .
.
Relations
For 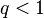 , a function that is closely related is
, a function that is closely related is
Here, 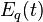 is a special case of the basic hypergeometric series:
is a special case of the basic hypergeometric series:
References
- F. H. Jackson (1908), On q-functions and a certain difference operator, Trans. Roy. Soc. Edin., 46 253-281.
- Exton, H. (1983), q-Hypergeometric Functions and Applications, New York: Halstead Press, Chichester: Ellis Horwood, 1983, ISBN 0853124914, ISBN 0470274530, ISBN 978-0470274538
- Gasper G., and Rahman, M. (2004), Basic Hypergeometric Series, Cambridge University Press, 2004, ISBN 0521833574
![e_q(z)=
\sum_{n=0}^\infty \frac{z^n}{[n]_q!} =
\sum_{n=0}^\infty \frac{z^n (1-q)^n}{(q;q)_n} =
\sum_{n=0}^\infty z^n\frac{(1-q)^n}{(1-q^n)(1-q^{n-1}) \cdots (1-q)}](../I/m/e15c462a0b44434270ccf2f394fb799d.png)
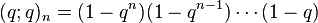
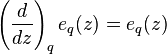
![\left(\frac{d}{dz}\right)_q z^n = z^{n-1} \frac{1-q^n}{1-q}
=[n]_q z^{n-1}.](../I/m/23a1aaaf482ca1996693456a7858adec.png)