q-Weibull distribution
|
Probability density function
| |
|
Cumulative distribution function
| |
| Parameters |
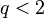 shape (real) shape (real) 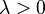 rate (real) rate (real) 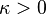 shape (real) shape (real) |
|---|---|
| Support |
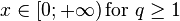 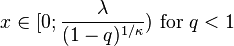 |
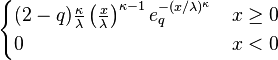 | |
| CDF |
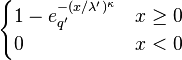 |
| Mean | (see article) |
In statistics, the q-Weibull distribution is a probability distribution that generalizes the Weibull distribution and the Lomax distribution (Pareto Type II). It is one example of a Tsallis distribution.
Characterization
Probability density function
The probability density function of a q-Weibull random variable is:[1]
where q < 2, 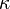 > 0 are shape parameters and λ > 0 is the scale parameter of the distribution and
> 0 are shape parameters and λ > 0 is the scale parameter of the distribution and
is the q-exponential[1][2][3]
Cumulative distribution function
The cumulative distribution function of a q-Weibull random variable is:
where
Mean
The mean of the q-Weibull distribution is
where 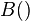 is the Beta function and
is the Beta function and 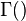 is the Gamma function. The expression for the mean is a continuous function of q over the range of definition for which it is finite.
is the Gamma function. The expression for the mean is a continuous function of q over the range of definition for which it is finite.
Relationship to other distributions
The q-Weibull is equivalent to the Weibull distribution when q = 1 and equivalent to the q-exponential when 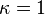
The q-Weibull is a generalization of the Weibull, as it extends this distribution to the cases of finite support (q < 1) and to include heavy tail distributions 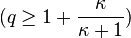 .
.
The q-Weibull is a generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support and adds the 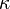 parameter. The Lomax parameters are:
parameter. The Lomax parameters are:
As the Lomax distribution is a shifted version of the Pareto distribution, the q-Weibull for 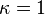 is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:
is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:
See also
References
- ↑ 1.0 1.1 Picoli, S. Jr.; Mendes, R. S.; Malacarne, L. C. (2008). "q-exponential, Weibull, and q-Weibull distributions: an empirical analysis". arXiv:cond-mat. Retrieved 9 June 2014.
- ↑ Naudts, Jan (2010). "The q-exponential family in statistical physics". J. Phys. Conf. Ser. (IOP Publishing) 201. doi:10.1088/1742-6596/201/1/012003. Retrieved 9 June 2014.
- ↑ "On a q-Central Limit Theorem Consistent with Nonextensive Statistical Mechanics". Milan j. math. 76. 2008. doi:10.1007/s00032-008-0087-y. Retrieved 9 June 2014.


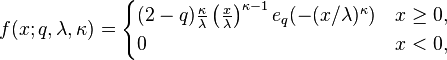
![e_q(x) = \begin{cases}
\exp(x) & \text{if }q=1, \\[6pt]
[1+(1-q)x]^{1/(1-q)} & \text{if }q \ne 1 \text{ and } 1+(1-q)x >0, \\[6pt]
0^{1/(1-q)} & \text{if }q \ne 1\text{ and }1+(1-q)x \le 0, \\[6pt]
\end{cases}](../I/m/6ae43c2f2a8eac9ca5fc5bd6ef5bebdc.png)
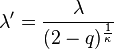
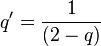
![\mu(q,\kappa,\lambda) =
\begin{cases}
\lambda\,\left(2+\frac{1}{1-q}+\frac{1}{\kappa}\right)(1-q)^{-\frac{1}{\kappa}}\,B\left[1+\frac{1}{\kappa},2+\frac{1}{1-q}\right]& q<1 \\
\lambda\,\Gamma(1+\frac{1}{\kappa}) & q=1\\
\lambda\,(2 - q) (q-1)^{-\frac{1+\kappa}{\kappa}}\,B\left[1+\frac{1}{\kappa}, -\left(1+\frac{1}{q-1}+\frac{1}{\kappa}\right)\right] & 1<q<1+\frac{1+2\kappa}{1+\kappa}\\
\infty & 1+\frac{\kappa}{\kappa+1}\le q<2
\end{cases}](../I/m/49917626b8b41e5bceaa5ed4a9f62db3.png)
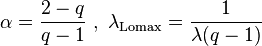
![\text{If } X \sim \mathrm{qWeibull}(q,\lambda,\kappa = 1) \text{ and } Y \sim \left[\text{Pareto}
\left(
x_m = {1 \over {\lambda (q-1)}}, \alpha = { {2-q} \over {q-1}}
\right) -x_m
\right],
\text{ then } X \sim Y \,](../I/m/d09fcce46baa7506fde04fde7f55f491.png)