q-Racah polynomials
In mathematics, the q-Racah polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by Askey & Wilson (1979). Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
Definition
The polynomials are given in terms of basic hypergeometric functions and the Pochhammer symbol by
![p_n(q^{-x}+q^{x+1}cd;a,b,c,d;q) = {}_4\phi_3\left[\begin{matrix} q^{-n} &abq^{n+1}&q^{-x}&q^{x+1}cd\\
aq&bdq&cq\\ \end{matrix};q;q\right]](../I/m/eeabd86662d80805eee7ebbcf540a2d8.png)
They are sometimes given with changes of variables as
![W_n(x;a,b,c,N;q) = {}_4\phi_3\left[\begin{matrix} q^{-n} &abq^{n+1}&q^{-x}&cq^{x-n}\\
aq&bcq&q^{-N}\\ \end{matrix};q;q\right]](../I/m/033f5a33887e9b5c4f0a9d1d05e871cc.png)
Relation to other polynomials
q-Racah polynomials→Racah polynomials
Gallery
 Q-Racah function abs complex 3D PLOT |
 Q-Racah function Im complex 3D PLOT |
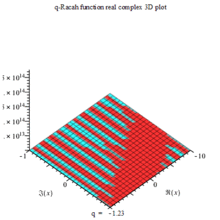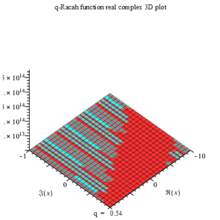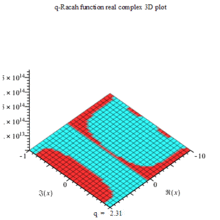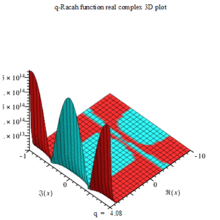 Q-Racah function re density PLOT |
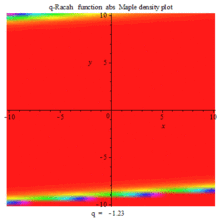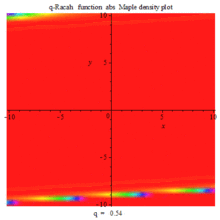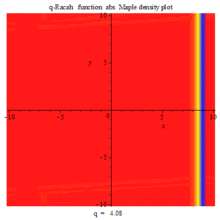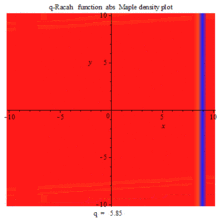 Q-Racah function abs density PLOT |
 Q-Racah function Im density PLOT |
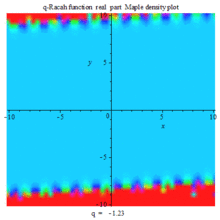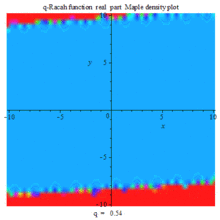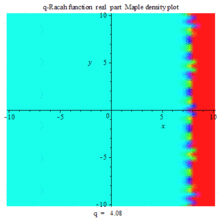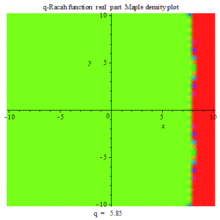 Q-Racah function re density PLOT |
References
- Askey, Richard; Wilson, James (1979), "A set of orthogonal polynomials that generalize the Racah coefficients or 6-j symbols", SIAM Journal on Mathematical Analysis 10 (5): 1008–1016, doi:10.1137/0510092, ISSN 0036-1410, MR 541097
- Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications 96 (2nd ed.), Cambridge University Press, doi:10.2277/0521833574, ISBN 978-0-521-83357-8, MR 2128719
- Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F. (2010), Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-05014-5, ISBN 978-3-642-05013-8, MR 2656096
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), http://dlmf.nist.gov/18
|contribution-url=missing title (help), in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248