q-Hahn polynomials

In mathematics, the q-Hahn polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme. Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.

Definition

The polynomials are given in terms of basic hypergeometric functions and the Pochhammer symbol by $Q_n(x;a,b,N;q)=\;_{3}\phi_2\left[\begin{matrix} q^-n & abq^n+1 & x \\ aq & q^-N \end{matrix} ; q,q \right]$

Relation to other polynomials

q-Hahn polynomials→ Quantum q-Krawtchouk polynomials：

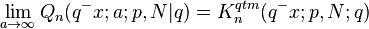
$\lim_{a \to \infty}Q_{n}(q^-{x};a;p,N|q)=K_{n}^{qtm}(q^-{x};p,N;q)$

q-Hahn polynomials→ Hahn polynomials

make the substitution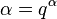 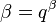$\alpha=q^{\alpha}$ , $\beta=q^{\beta}$ into definition of q-Hahn polynomials, and find the limit q→1, we obtain

： $_3F_2([-n, \alpha+\beta+n+1, -x], [\alpha+1, -N], 1)$ ，which is exactly Hahn polynomials.

Gallery

Q-HAHN ABS COMPLEX3D MAPLE PLOT

Q-HAHN IM COMPLEX3D MAPLE PLOT

Q-HAHN RE COMPLEX3D MAPLE PLOT

Q-HAHN ABS DENSITY MAPLE PLOT

Q-HAHN IM DENSITY MAPLE PLOT

Q-HAHN RE DENSITY MAPLE PLOT

References

Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications 96 (2nd ed.), Cambridge University Press, doi:10.2277/0521833574, ISBN 978-0-521-83357-8, MR 2128719
Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F. (2010), Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-05014-5, ISBN 978-3-642-05013-8, MR 2656096
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), http://dlmf.nist.gov/18 |contribution-url= missing title (help), in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248