Purification of quantum state
In quantum mechanics, especially quantum information, purification refers to the fact that every mixed state acting on finite-dimensional Hilbert spaces can be viewed as the reduced state of some pure state.
In purely linear algebraic terms, it can be viewed as a statement about positive-semidefinite matrices.
Statement
Let ρ be a density matrix acting on a Hilbert space 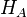 of finite dimension n. Then there exist a Hilbert space
of finite dimension n. Then there exist a Hilbert space 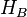 and a pure state
and a pure state 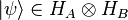 such that the partial trace of
such that the partial trace of 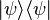 with respect to
with respect to 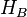
We say that 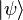 is the purification of
is the purification of  .
.
Proof
A density matrix is by definition positive semidefinite. So ρ can be diagonalized and written as 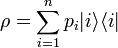 for some basis
for some basis 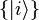 . Let
. Let 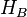 be another copy of the n-dimensional Hilbert space with an orthonormal basis
be another copy of the n-dimensional Hilbert space with an orthonormal basis 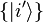 . Define
. Define 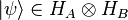 by
by
Direct calculation gives
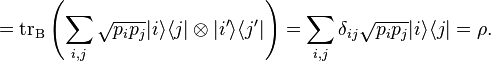
This proves the claim.
Note
- The vectorial pure state
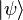 is in the form specified by the Schmidt decomposition.
is in the form specified by the Schmidt decomposition.
- Since square root decompositions of a positive semidefinite matrix are not unique, neither are purifications.
- In linear algebraic terms, a square matrix is positive semidefinite if and only if it can be purified in the above sense. The if part of the implication follows immediately from the fact that the partial trace of a positive map remains a positive map.
An application: Stinespring's theorem
By combining Choi's theorem on completely positive maps and purification of a mixed state, we can recover the Stinespring dilation theorem for the finite-dimensional case.
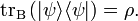
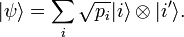
![\operatorname{tr_B} \left( | \psi \rangle \langle \psi | \right )=
\operatorname{tr_B} \left[\left( \sum_{i} \sqrt{p_i} |i \rangle \otimes | i' \rangle \right ) \left( \sum_{j} \sqrt{p_j} \langle j | \otimes \langle j'| \right) \right]](../I/m/915e964a3a355fb76cdb9b5e718b74b6.png)