Publicly Verifiable Secret Sharing
In cryptography, a secret sharing scheme is publicly verifiable (PVSS) if it is a verifiable secret sharing scheme and if any party involved can verify the validity of the shares distributed by the dealer.
In verifiable secret sharing (VSS) the object is to resist malicious players, such as
(i) a dealer sending incorrect shares to some or all of the participants, and
(ii) participants submitting incorrect shares during the reconstruction protocol,cf. [CGMA85].
In publicly verifiable secret sharing (PVSS), as introduced by Stadler [Sta96], it is an explicit goal that not just the participants can verify theirown shares, but that anybody can verify that the participants received correct shares. Hence, it is explicitly required that
can be verified publicly.
— Berry Schoenmakers. A Simple Publicly Verifiable Secret Sharing Scheme and its Application to Electronic Voting .
The method introduced here according to the paper by Chunming Tang, Dingyi Pei, Zhuo Liu, and Yong He is non-interactive and maintains this property throughout the protocol.
Initialization
The PVSS scheme dictates an initialization process in which:
- All system parameters are generated.
- Each participant must have a registered public key.
Excluding the initialization process, the PVSS consists of two phases:
Distribution
1.Distribution of secret  shares is performed by the dealer
shares is performed by the dealer  , which does the following:
, which does the following:
- The dealer creates
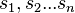 for each participant
for each participant 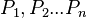 respectively.
respectively. - The dealer publishes the encrypted share
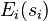 for each
for each 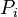 .
. - The dealer also publishes a string
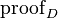 to show that each
to show that each 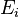 encrypts
encrypts 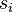
(note: 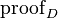 guarantees that the reconstruction protocol will result in the same
guarantees that the reconstruction protocol will result in the same  .
.
2. Verification of the shares:
- Anybody knowing the public keys for the encryption methods
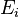 , can verify the shares.
, can verify the shares. - If one or more verifications fails the dealer fails and the protocol is aborted.
Reconstruction
1. Decryption of the shares:
- The Participants
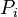 decrypts their share of the secret
decrypts their share of the secret 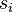 using
using 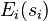 .
.
(note: fault-tolerance can be allowed here: it's not required that all participants succeed in decrypting 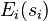 as long as a qualified set of participants are successful to decrypt
as long as a qualified set of participants are successful to decrypt 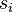 ).
).
- The participant release
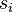 plus a string
plus a string 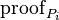 this shows the released share is correct.
this shows the released share is correct.
2. Pooling the shares:
- Using the strings
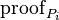 to exclude the participants which are dishonest or failed to decrypt
to exclude the participants which are dishonest or failed to decrypt 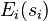 .
. - Reconstruction
 can be done from the shares of any qualified set of participants.
can be done from the shares of any qualified set of participants.
Chaums and Pedersen Scheme
A proposed protocol proving: 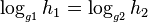 :
:
- The prover chooses a random
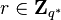
- The verifier send a random challenge
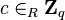
- The prover responds with
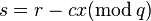
- The verifier checks
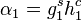 and
and 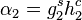
Denote this protocol as: 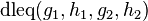
A generalization of 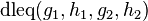 is denoted as:
is denoted as: 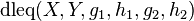 where as:
where as: 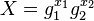 and
and 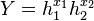 :
:
- The prover chooses a random
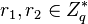 and sends
and sends 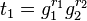 and
and 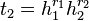
- The verifier send a random challenge
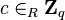 .
. - The prover responds with
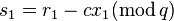 ,
, 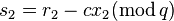 .
. - The verifier checks
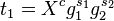 and
and 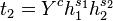
The Chaums and Pedersen method is an interactive method and needs some modification to be used in a non-interactive way:
Replacing the randomly chosen  by a 'secure hash' function with
by a 'secure hash' function with  as input value.
as input value.
See also
References
- Markus Stadler, Publicly Verifiable Secret Sharing
- Berry Schoenmakers, A Simple Publicly Verifiable Secret Sharing Scheme and its Application to Electronic Voting, Advances in Cryptology—CRYPTO, 1999, pp. 148–164