Pseudorandom generators for polynomials
In theoretical computer science, a pseudorandom generator for low-degree polynomials is an efficient procedure that maps a short truly random seed to a longer pseudorandom string in such a way that low-degree polynomials cannot distinguish the output distribution of the generator from the truly random distribution. That is, evaluating any low-degree polynomial at a point determined by the pseudorandom string is statistically close to evaluating the same polynomial at a point that is chosen uniformly at random.
Pseudorandom generators for low-degree polynomials are a particular instance of pseudorandom generators for statistical tests, where the statistical tests considered are evaluations of low-degree polynomials.
Definition
A pseudorandom generator 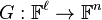 for polynomials of degree
for polynomials of degree 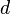 over a finite field
over a finite field 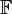 is an efficient procedure that maps a sequence of
is an efficient procedure that maps a sequence of 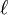 field elements to a sequence of
field elements to a sequence of  field elements such that any
field elements such that any  -variate polynomial over
-variate polynomial over 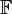 of degree
of degree 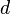 is fooled by the output distribution of
is fooled by the output distribution of  .
In other words, for every such polynomial
.
In other words, for every such polynomial 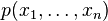 , the statistical distance between the distributions
, the statistical distance between the distributions 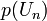 and
and 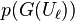 is at most a small
is at most a small  , where
, where 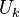 is the uniform distribution over
is the uniform distribution over 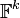 .
.
Construction
The case 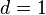 corresponds to pseudorandom generators for linear functions and is solved by small-bias generators.
For example, the construction of Naor & Naor (1990) achieves a seed length of
corresponds to pseudorandom generators for linear functions and is solved by small-bias generators.
For example, the construction of Naor & Naor (1990) achieves a seed length of 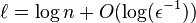 , which is optimal up to constant factors.
, which is optimal up to constant factors.
Bogdanov & Viola (2007) conjectured that the sum of small-bias generators fools low-degree polynomials and were able to prove this under the Gowers inverse conjecture.
Lovett (2009) proved unconditionally that the sum of 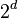 small-bias spaces fools polynomials of degree
small-bias spaces fools polynomials of degree 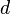 .
Viola (2008) proves that, in fact, taking the sum of only
.
Viola (2008) proves that, in fact, taking the sum of only 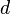 small-bias generators is sufficient to fool polynomials of degree
small-bias generators is sufficient to fool polynomials of degree 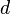 .
The analysis of Viola (2008) gives a seed length of
.
The analysis of Viola (2008) gives a seed length of 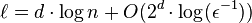 .
.
References
- Bogdanov, Andrej; Viola, Emanuele (2007), "Pseudorandom Bits for Polynomials", Proceedings of the 48th Annual Symposium on Foundations of Computer Science (FOCS 2007): 41–51, doi:10.1109/FOCS.2007.56
- Lovett, Shachar (2009), "Unconditional Pseudorandom Generators for Low Degree Polynomials", Theory of Computing 5 (3): 69–82, doi:10.4086/toc.2009.v005a003
- Naor, Joseph; Naor, Moni (1990), "Small-bias Probability Spaces: efficient constructions and Applications", Proceedings of the 22nd annual ACM symposium on Theory of computing, STOC 1990: 213–223, doi:10.1145/100216.100244, ISBN 0897913612
- Viola, Emanuele (2008), "The sum of d small-bias generators fools polynomials of degree d", Proceedings of the 23rd Annual Conference on Computational Complexity (CCC 2008): 124–127, doi:10.1109/CCC.2008.16