Pseudopotential
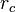 .
.In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering. The pseudopotential approximation was first introduced by Hans Hellmann in the 1934.[1]
Atomic physics
The pseudopotential is an attempt to replace the complicated effects of the motion of the core (i.e. non-valence) electrons of an atom and its nucleus with an effective potential, or pseudopotential, so that the Schrödinger equation contains a modified effective potential term instead of the Coulombic potential term for core electrons normally found in the Schrödinger equation.
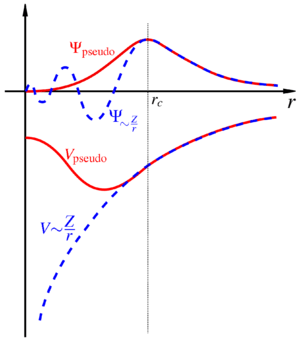
The pseudopotential is an effective potential constructed to replace the atomic all-electron potential (full-potential) such that core states are eliminated and the valence electrons are described by pseudo-wavefunctions with significantly fewer nodes. This allows the pseudo-wavefunctions to be described with far fewer Fourier modes, thus making plane-wave basis sets practical to use. In this approach usually only the chemically active valence electrons are dealt with explicitly, while the core electrons are 'frozen', being considered together with the nuclei as rigid non-polarizable ion cores. It is possible to self-consistently update the pseudopotential with the chemical environment that it is embedded in, having the effect of relaxing the frozen core approximation, although this is rarely done.
First-principles pseudopotentials are derived from an atomic reference state, requiring that the pseudo- and all-electron valence eigenstates have the same energies and amplitude (and thus density) outside a chosen core cut-off radius 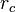 .
.
Pseudopotentials with larger cut-off radius are said to be softer, that is more rapidly convergent, but at the same time less transferable, that is less accurate to reproduce realistic features in different environments.
Motivation:
- Reduction of basis set size
- Reduction of number of electrons
- Inclusion of relativistic and other effects
Approximations:
- One-electron picture.
- The small-core approximation assumes that there is no significant overlap between core and valence wave-function. Nonlinear core corrections[2] or "semicore" electron inclusion[3] deal with situations where overlap is non-negligible.
Early applications of pseudopotentials to atoms and solids based on attempts to fit atomic spectra achieved only limited success. Solid-state pseudopotentials achieved their present popularity largely because of the successful fits by Walter Harrison to the nearly free electron Fermi surface of aluminum (1958) and by James C. Phillips to the covalent energy gaps of silicon and germanium (1958). Phillips and coworkers (notably Marvin L. Cohen and coworkers) later extended this work to many other semiconductors, in what they called "semiempirical pseudopotentials". [4]
Norm-conserving and ultrasoft first-principles pseudopotentials
Norm-conserving and ultrasoft are the two most common forms of pseudopotential used in modern plane-wave electronic structure codes. They allow a basis-set with a significantly lower cut-off (the frequency of the highest Fourier mode) to be used to describe the electron wavefunctions and so allow proper numerical convergence with reasonable computing resources. An alternative would be to augment the basis set around nuclei with atomic-like functions, as is done in LAPW. First-principles pseudopotentials are usually non-local, meaning that different angular momentum states feel different effective potentials, giving a potential operator of the form:
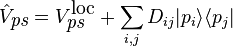
where 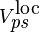 is the pseudopotential's local potential,
is the pseudopotential's local potential, 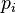 projects on to some angular momentum and radial state and
projects on to some angular momentum and radial state and 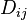 is some matrix specific to the pseudopotential.
is some matrix specific to the pseudopotential.
Norm-conserving pseudopotentials are constructed to enforce the condition that, inside the cut-off radius, the norm of each pseudo-wavefunction be identical to its corresponding all-electron wavefunction:[5]
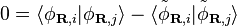 ,
,
where 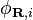 and
and 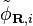 are the all-electron and pseudo reference states for the pseudopotential on atom
are the all-electron and pseudo reference states for the pseudopotential on atom 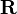 and are identical to one another outside the pseudopotential cut-off radius,
and are identical to one another outside the pseudopotential cut-off radius, 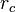 .
.
Ultrasoft pseudopotentials relax the norm-conserving constraint to reduce the necessary basis-set size further at the expense of introducing a generalized eigenvalue problem.[6] With a non-zero difference in norms we can now define:
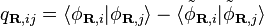 ,
,
and so a normalised eigenstate of the pseudo Hamiltonian now obeys the generalized equation
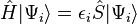 ,
,
where the operator 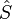 is defined as
is defined as
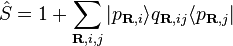 ,
,
where 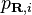 are projectors that form a dual basis with the pseudo reference states inside the cut-off radius, and are zero outside:
are projectors that form a dual basis with the pseudo reference states inside the cut-off radius, and are zero outside:
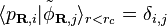 .
.
A related technique[7] is the projector augmented wave (PAW) method.
Fermi pseudopotential
Enrico Fermi introduced a pseudopotential,  , to describe the scattering of a free neutron by a nucleus.[8] The scattering is assumed to be s-wave scattering, and therefore spherically symmetric. Therefore, the potential is given as a function of radius,
, to describe the scattering of a free neutron by a nucleus.[8] The scattering is assumed to be s-wave scattering, and therefore spherically symmetric. Therefore, the potential is given as a function of radius,  :
:
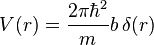 ,
,
where 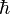 is the Planck constant divided by
is the Planck constant divided by 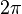 ,
,  is the mass,
is the mass, 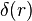 is the Dirac delta function,
is the Dirac delta function,  is the neutron scattering length, and
is the neutron scattering length, and 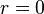 the center of mass of the nucleus.[9] The Fourier transform of this
the center of mass of the nucleus.[9] The Fourier transform of this 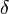 -function leads to the constant neutron form factor.
-function leads to the constant neutron form factor.
Phillips pseudopotential
James C Phillips developed a simplified pseudopotential while at Bell Labs useful for describing silicon and germanium.
Literature
- Hellmann, Hans (1935), "A New Approximation Method in the Problem of Many Electrons", Journal of Chemical Physics (Karpow‐Institute for Physical Chemistry, Moscow) 3: 61, Bibcode:1935JChPh...3...61H, doi:10.1063/1.1749559, ISSN 0021-9606
- Hellmann, H.; Kassatotschkin, W. (1936), "Metallic Binding According to the Combined Approximation Procedure", Journal of Chemical Physics (Karpow‐Institute for Physical Chemistry, Moscow) 4: 324, Bibcode:1936JChPh...4..324H, doi:10.1063/1.1749851, ISSN 0021-9606
- Harrison, Walter Ashley (1966), Pseudopotentials in the theory of metals, Frontiers in Physics (25), University of Virginia
- Brust, David (1968), Alder, Berni, ed., "The Pseudopotential Method and the Single-Particle Electronic Excitation Spectra of Crystals", Methods in Computational Physics (New York: Academic Press) 8: 33–61, ISSN 0076-6860
- Heine, Volker (1970), "The Pseudopotential Concept", Solid State Physics (Academic Press) 24: 1–36, doi:10.1016/S0081-1947(08)60069-7
- Pickett, Warren E. (April 1989), "Pseudopotential methods in condensed matter applications", Computer Physics reports 9 (3): 115–197, Bibcode:1989CoPhR...9..115P, doi:10.1016/0167-7977(89)90002-6
Resources
- NNIN Virtual Vault for Pseudopotentials : This webpage maintained by the NNIN/C provides a searchable database of pseudopotentials for density functional codes as well as links to pseudopotential generators, converters, and other online databases.
- Vanderbilt Ultra-Soft Pseudopotential Site : Website of David Vanderbilt with links to codes that implement ultrasoft pseudopotentials and libraries of generated pseudopotentials.
References
- ↑ Schwerdtfeger, P. (August 2011), "The Pseudopotential Approximation in Electronic Structure Theory", ChemPhysChem, doi:10.1002/cphc.201100387
- ↑ Louie, Steven G.; Froyen, Sverre; Cohen, Marvin L. (August 1982), "Nonlinear ionic pseudopotentials in spin-density-functional calculations", Physical Rev. B (American Physical Society) 26 (4): 1738–1742, Bibcode:1982PhRvB..26.1738L, doi:10.1103/PhysRevB.26.1738
- ↑ Reis, Carlos L.; Pacheco, J. M.; Martins, José Luís (October 2003), "First-principles norm-conserving pseudopotential with explicit incorporation of semicore states", Physical Review B (American Physical Society) 68 (15): 155111, Bibcode:2003PhRvB..68o5111R, doi:10.1103/PhysRevB.68.155111
- ↑ M. L. Cohen, J. R. Chelikowsky, "Electronic Structure and Optical Spectra of Semiconductors", (Springer Verlag, Berlin 1988)
- ↑ Bachelet, G. B.; Hamann, D. R.; Schlüter, M. (October 1982), "Pseudopotentials that work: From H to Pu", Physical Review B (American Physical Society) 26 (8): 4199–4228, Bibcode:1982PhRvB..26.4199B, doi:10.1103/PhysRevB.26.4199
- ↑ Vanderbilt, David (April 1990), "Soft self-consistent pseudopotentials in a generalized eigenvalue formalism", Physical Review B (American Physical Society) 41 (11): 7892–7895, Bibcode:1990PhRvB..41.7892V, doi:10.1103/PhysRevB.41.7892
- ↑ Kresse, G.; Joubert, D. (1999). "From ultrasoft pseudopotentials to the projector augmented-wave method". Bibcode:1999PhRvB..59.1758K. doi:10.1103/PhysRevB.59.1758.
- ↑ E. Fermi (July 1936), "Motion of neutrons in hydrogenous substances", Ricerca Scientifica 7: 13–52
- ↑ Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover Publications (1996) ISBN 0-486-69447-X