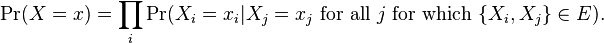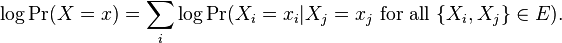Pseudolikelihood
In statistical theory, a pseudolikelihood is an approximation to the joint probability distribution of a collection of random variables. The practical use of this is that it can provide an approximation to the likelihood function of a set of observed data which may either provide a computationally simpler problem for estimation, or may provide a way of obtaining explicit estimates of model parameters.
The pseudolikelihood approach was introduced by Julian Besag[1] in the context of analysing data having spatial dependence.
Definition
Given a set of random variables 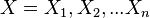 and a set
and a set  of dependencies between these random variables, where
of dependencies between these random variables, where 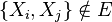 implies
implies  is conditionally independent of
is conditionally independent of 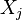 given
given  's neighbors, the pseudolikelihood of
's neighbors, the pseudolikelihood of 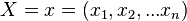 is
is
Here  is a vector of variables,
is a vector of variables,  is a vector of values. The expression
is a vector of values. The expression 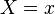 above means that each variable
above means that each variable  in the vector
in the vector  has a corresponding value
has a corresponding value 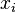 in the vector
in the vector  . The expression
. The expression 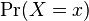 is the probability that the vector of variables
is the probability that the vector of variables  has values equal to the vector
has values equal to the vector  . Because situations can often be described using state variables ranging over a set of possible values, the expression
. Because situations can often be described using state variables ranging over a set of possible values, the expression 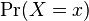 can therefore represent the probability of a certain state among all possible states allowed by the state variables.
can therefore represent the probability of a certain state among all possible states allowed by the state variables.
The pseudo-log-likelihood is a similar measure derived from the above expression. Thus
One use of the pseudolikelihood measure is as an approximation for inference about a Markov or Bayesian network, as the pseudolikelihood of an assignment to  may often be computed more efficiently than the likelihood, particularly when the latter may require marginalization over a large number of variables.
may often be computed more efficiently than the likelihood, particularly when the latter may require marginalization over a large number of variables.
Properties
Use of the pseudolikelihood in place of the true likelihood function in a maximum likelihood analysis can lead to good estimates, but a straightforward application of the usual likelihood techiques to derive information about estimation uncertainty, or for significance testing, would in general be incorrect.[2]