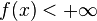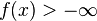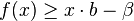Proper convex function
In mathematical analysis (in particular convex analysis) and optimization, a proper convex function is a convex function f taking values in the extended real number line such that
for at least one x and
for every x. That is, a convex function is proper if its effective domain is nonempty and it never attains 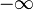 .[1] Convex functions that are not proper are called improper convex functions.[2]
.[1] Convex functions that are not proper are called improper convex functions.[2]
A proper concave function is any function g such that 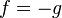 is a proper convex function.
is a proper convex function.
Properties
For every proper convex function f on Rn there exist some b in Rn and β in R such that
for every x.
The sum of two proper convex functions is not necessarily proper or convex. For instance if the sets 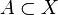 and
and 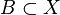 are non-empty convex sets in the vector space X, then the indicator functions
are non-empty convex sets in the vector space X, then the indicator functions 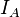 and
and 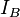 are proper convex functions, but if
are proper convex functions, but if 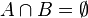 then
then  is identically equal to
is identically equal to 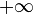 .
.
The infimal convolution of two proper convex functions is convex but not necessarily proper convex.[3]
References
- ↑ Aliprantis, C.D.; Border, K.C. (2007). Infinite Dimensional Analysis: A Hitchhiker's Guide (3 ed.). Springer. p. 254. doi:10.1007/3-540-29587-9. ISBN 978-3-540-32696-0.
- ↑ Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. p. 24. ISBN 978-0-691-01586-6.
- ↑ Ioffe, Aleksandr Davidovich; Tikhomirov, Vladimir Mikhaĭlovich (2009), Theory of extremal problems, Studies in Mathematics and its Applications 6, North-Holland, p. 168, ISBN 9780080875279.