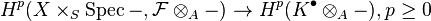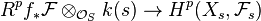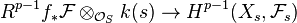Proper base change theorem
- There is also a proper base change theorem in topology. For that, see base change map.
In algebraic geometry, there are at least two versions of proper base change theorems: one for ordinary cohomology and the other for étale cohomology.
In ordinary cohomology
The proper base change theorem states the following: let 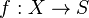 be a proper morphism between noetherian schemes, and
be a proper morphism between noetherian schemes, and  S-flat coherent sheaf on
S-flat coherent sheaf on  . If
. If 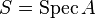 , then there is a finite complex
, then there is a finite complex 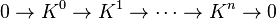 of finitely generated projective A-modules and a natural isomorphism of functors
of finitely generated projective A-modules and a natural isomorphism of functors
on the category of  -algebras.
-algebras.
There are several corollaries to the theorem, some of which are also referred to as proper base change theorems: (the higher direct image 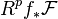 is coherent since f is proper.)
is coherent since f is proper.)
Corollary 1 (semicontinuity theorem): Let f and  as in the theorem (but S may not be affine). Then we have:
as in the theorem (but S may not be affine). Then we have:
- (i) For each
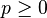 , the function
, the function 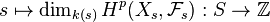 is upper semicontinuous.
is upper semicontinuous. - (ii) The function
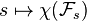 is locally constant, where
is locally constant, where 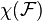 denotes the Euler characteristic.
denotes the Euler characteristic.
Corollary 2: Assume S is reduced and connected. Then for each 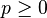 the following are equivalent
the following are equivalent
- (i)
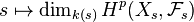 is constant.
is constant. - (ii)
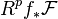 is locally free and the natural map
is locally free and the natural map
- is an isomorphism for all
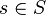 .
. - Furthermore, if these conditions hold, then the natural map
- is an isomorphism for all
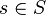 .
.
Corollary 3: Assume that for some p 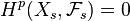 for all
for all 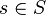 . Then
the natural map
. Then
the natural map
- is an isomorphism for all
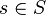 .
.
In étale cohomology
In nutshell, the proper base change theorem states that the higher direct image 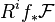 of a torsion sheaf
of a torsion sheaf  along a proper morphism f commutes with base change. A closely related, the finiteness theorem states that the étale cohomology groups of a constructible sheaf on a complete variety are finite. Two theorems are usually proved simultaneously.
along a proper morphism f commutes with base change. A closely related, the finiteness theorem states that the étale cohomology groups of a constructible sheaf on a complete variety are finite. Two theorems are usually proved simultaneously.
Theorem (finiteness): Let X be a variety over a separably closed field and  a constructible sheaf on
a constructible sheaf on 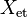 . Then
. Then 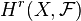 are finite in each of the following cases: (i) X is complete, or (ii)
are finite in each of the following cases: (i) X is complete, or (ii)  has no p-torsion, where p is the characteristic of k.
has no p-torsion, where p is the characteristic of k.
References
- Robin Hartshorne, Algebraic Geometry.
- David Mumford, Abelian Varieties.
- Vakil's notes
- SGA 4
- Milne, Étale cohomology
- Gabber, "Finiteness theorems for étale cohomology of excellent schemes"