Proofs of trigonometric identities
Proofs of trigonometric identities are used to show relations between trigonometric functions. This article will list trigonometric identities and prove them.
Elementary trigonometric identities
Definitions
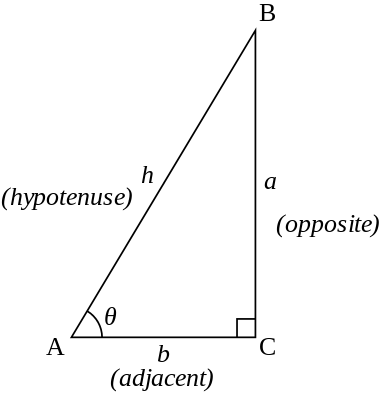
Referring to the diagram at the right, the six trigonometric functions of θ are:
Ratio identities
The following identities are trivial algebraic consequences of these definitions and the division identity.
They rely on multiplying or dividing the numerator and denominator of fractions by a variable. Ie,
Or
Complementary angle identities
Two angles whose sum is π/2 radians (90 degrees) are complementary. In the diagram, the angles at vertices A and B are complementary, so we can exchange a and b, and change θ to π/2 − θ, obtaining:
Pythagorean identities
Identity 1:
The following two results follow from this and the ratio identities. To obtain the first, divide both sides of 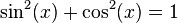 by
by  ; for the second, divide by
; for the second, divide by 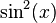 .
.
Similarly
Identity 2:
The following accounts for all three reciprocal functions.
Proof 2:
Refer to the triangle diagram above. Note that  by Pythagorean theorem.
by Pythagorean theorem.
Substituting with appropriate functions -
Rearranging gives:
Angle sum identities
Sine

Draw a horizontal line (the x-axis); mark an origin O. Draw a line from O at an angle 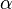 above the horizontal line and a second line at an angle
above the horizontal line and a second line at an angle 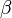 above that; the angle between the second line and the x-axis is
above that; the angle between the second line and the x-axis is  .
.
Place P on the line defined by  at a unit distance from the origin.
at a unit distance from the origin.
Let PQ be a line perpendicular to line defined by angle 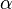 , drawn from point Q on this line to point P.
, drawn from point Q on this line to point P.  OQP is a right angle.
OQP is a right angle.
Let QA be a perpendicular from point A on the x-axis to Q and PB be a perpendicular from point B on the x-axis to P.  OAQ and OBP are right angles.
OAQ and OBP are right angles.
Draw QR parallel to the x-axis.
Now angle 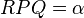 (because
(because  ,
making
,
making  , and finally
, and finally 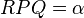 )
)

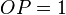


 , so
, so 
 , so
, so 

By substituting 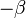 for
for 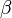 and using Symmetry, we also get:
and using Symmetry, we also get:
Another simple "proof" can be given using Euler's formula known from complex analysis: Euler's formula is:
Although it is more precise to say that Euler's formula entails the trigonometric identities, it follows that for angles 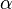 and
and 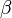 we have:
we have:
Also using the following properties of exponential functions:
Evaluating the product:
Equating real and imaginary parts:
Cosine
Using the figure above,
 , so
, so 
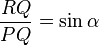 , so
, so 
By substituting 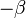 for
for 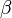 and using Symmetry, we also get:
and using Symmetry, we also get:
Also, using the complementary angle formulae,
Tangent and cotangent
From the sine and cosine formulae, we get
Dividing both numerator and denominator by 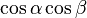 , we get
, we get
Subtracting  from
from 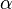 , using
, using  ,
,
Similarly from the sine and cosine formulae, we get
Then by dividing both numerator and denominator by  , we get
, we get
Or, using  ,
,
Using  ,
,
Double-angle identities
From the angle sum identities, we get
and
The Pythagorean identities give the two alternative forms for the latter of these:
The angle sum identities also give
It can also be proved using Euler's formula
Squaring both sides yields
But replacing the angle with its doubled version, which achieves the same result in the left side of the equation, yields
It follows that
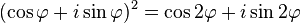 .
.
Expanding the square and simplifying on the left hand side of the equation gives
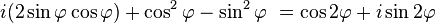 .
.
Because the imaginary and real parts have to be the same, we are left with the original identities
 ,
,
and also
 .
.
Half-angle identities
The two identities giving the alternative forms for cos 2θ lead to the following equations:
The sign of the square root needs to be chosen properly—note that if π is added to θ, the quantities inside the square roots are unchanged, but the left-hand-sides of the equations change sign. Therefore the correct sign to use depends on the value of θ.
For the tan function, the equation is:
Then multiplying the numerator and denominator inside the square root by (1 + cos θ) and using Pythagorean identities leads to:
Also, if the numerator and denominator are both multiplied by (1 - cos θ), the result is:
This also gives:
Similar manipulations for the cot function give:
Miscellaneous -- the triple tangent identity
If  half circle (for example,
half circle (for example, 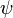 ,
, 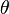 and
and  are the angles of a triangle),
are the angles of a triangle),
Proof:[1]
Miscellaneous -- the triple cotangent identity
If 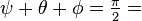 quarter circle,
quarter circle,
 .
.
Proof:
Replace each of 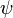 ,
, 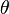 , and
, and  with their complementary angles, so cotangents turn into tangents and vice versa.
with their complementary angles, so cotangents turn into tangents and vice versa.
Given
so the result follows from the triple tangent identity.
Prosthaphaeresis identities
Proof of sine identities
First, start with the sum-angle identities:
By adding these together,
Similarly, by subtracting the two sum-angle identities,
Let 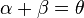 and
and  ,
,
 and
and 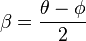
Substitute 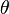 and
and 
Therefore,
Proof of cosine identities
Similarly for cosine, start with the sum-angle identities:
Again, by adding and subtracting
Substitute 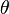 and
and  as before,
as before,
Inequalities

The figure at the right shows a sector of a circle with radius 1. The sector is θ/(2π) of the whole circle, so its area is θ/2.
The area of triangle OAD is AB/2, or sinθ/2. The area of triangle OCD is CD/2, or tanθ/2.
Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we have
This geometric argument applies if 0<θ<π/2. It relies on definitions of arc length and area, which act as assumptions, so it is rather a condition imposed in construction of trigonometric functions than a provable property.[2] For the sine function, we can handle other values. If θ>π/2, then θ>1. But sinθ≤1 (because of the Pythagorean identity), so sinθ<θ. So we have
For negative values of θ we have, by symmetry of the sine function
Hence
Identities involving calculus
Preliminaries
Sine and angle ratio identity
Proof: From the previous inequalities, we have, for small angles
 ,
,
Therefore,
 ,
,
Consider the right-hand inequality. Since
Multply through by 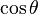
Combining with the left-hand inequality:
Taking 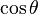 to the limit as
to the limit as 
Therefore,
Cosine and angle ratio identity
Proof:
The limits of those three quantities are 1, 0, and 1/2, so the resultant limit is zero.
Cosine and square of angle ratio identity
Proof:
As in the preceding proof,
The limits of those three quantities are 1, 1, and 1/2, so the resultant limit is 1/2.
Proof of Compositions of trig and inverse trig functions
All these functions follow from the Pythagorean trigonometric identity. We can prove for instance the function
Proof:
We start from
Then we divide this equation by 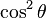
Then use the substitution  , also use the Pythagorean trigonometric identity:
, also use the Pythagorean trigonometric identity:
Then we use the identity ![\tan[\arctan(x)]\equiv x](../I/m/2e78e5a7be8d08e992309931467e1f2e.png)
See also
- List of trigonometric identities
- Bhaskara I's sine approximation formula
- Generating trigonometric tables
- Aryabhata's sine table
- Madhava's sine table
- Table of Newtonian series
- Madhava series
- Unit vector (explains direction cosines)
- Euler's formula
Notes
- ↑ http://mathlaoshi.com/tags/tangent-identity/ dead link
- ↑ Richman, Fred (March 1993). . "A Circular Argument". The College Mathematics Journal 24 (2): 160–162. doi:10.2307/2686787. Retrieved 3 November 2012.
References
- E. T. Whittaker and G. N. Watson. A course of modern analysis, Cambridge University Press, 1952






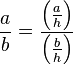












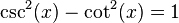









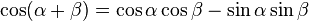





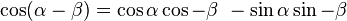
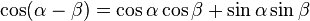



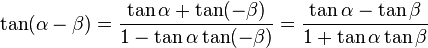


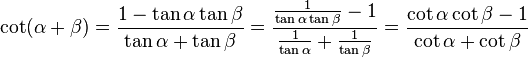

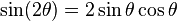



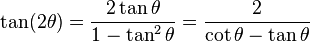














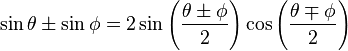
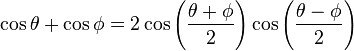

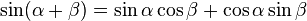
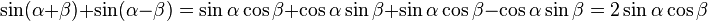


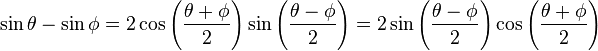
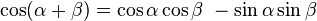
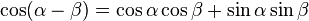


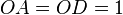
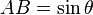




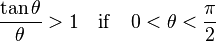
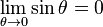
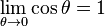


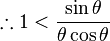

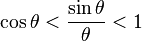



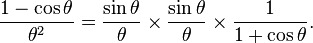
![\sin[\arctan(x)]=\frac{x}{\sqrt{1+x^2}}](../I/m/6b703c82a30a73cdbc55bab9b3dec503.png)
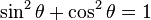
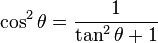
![1-\sin^2[\arctan(x)]=\frac{1}{\tan^2[\arctan(x)]+1}](../I/m/957d9c27bc577594e2ad79bfa74c613c.png)
![\sin[\arctan(x)]=\frac{x}{\sqrt{x^2+1}}](../I/m/d5241d86a69219ff4529dd0115bfbee8.png)