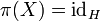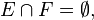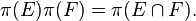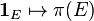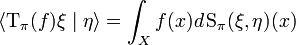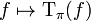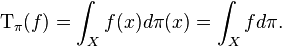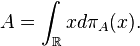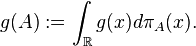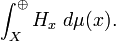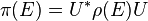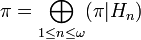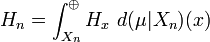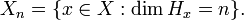Projection-valued measure

In mathematics, particularly in functional analysis, a projection-valued measure (PVM) is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a fixed Hilbert space. Projection-valued measures are formally similar to real-valued measures, except that their values are self-adjoint projections rather than real numbers. As in the case of ordinary measures, it is possible to integrate complex-valued functions with respect to a PVM; the result of such an integration is a linear operator on the given Hilbert space.

Projection-valued measures are used to express results in spectral theory, such as the important spectral theorem for self-adjoint operators. The Borel functional calculus for self-adjoint operators is constructed using integrals with respect to PVMs. In quantum mechanics, PVMs are the mathematical description of projective measurements. They are generalized by positive operator valued measures (POVMs) in the same sense that a mixed state or density matrix generalizes the notion of a pure state.

Formal definition

A projection-valued measure on a measurable space (X, M), where M is a σ-algebra of subsets of X, is a mapping π from M to the set of self-adjoint projections on a Hilbert space H such that

\pi(X) = \operatorname{id}_H \quad

and for every ξ, η ∈ H, the set-function

E \mapsto \langle \pi(E)\xi \mid \eta \rangle

is a complex measure on M (that is, a complex-valued countably additive function). We denote this measure by 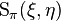\operatorname{S}_\pi(\xi, \eta).

If π is a projection-valued measure and

E \cap F = \emptyset,

then π(E), π(F) are orthogonal projections. From this follows that in general,

\pi(E) \pi(F) = \pi(E \cap F).

Example. Suppose (X, M, μ) is a measure space. Let π(E) be the operator of multiplication by the indicator function 1E on L2(X). Then π is a projection-valued measure.

Extensions of projection-valued measures, integrals and the spectral theorem

If π is a projection-valued measure on (X, M), then the map

\mathbf{1}_E \mapsto \pi(E)

extends to a linear map on the vector space of step functions on X. In fact, it is easy to check that this map is a ring homomorphism. This map extends in a canonical way to all bounded complex-valued measurable functions on X.

Theorem. For any bounded M-measurable function f on X, there is a unique bounded linear operator Tπ(f) such that

\langle \operatorname{T}_\pi(f) \xi \mid \eta \rangle = \int_X f(x) d \operatorname{S}_\pi (\xi,\eta)(x)

for all ξ, η ∈ H. Here, 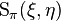\operatorname{S}_\pi (\xi,\eta) denotes the complex measure 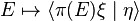E \mapsto \langle \pi(E)\xi \mid \eta \rangle from the definition of 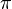\pi. The map

f \mapsto \operatorname{T}_\pi(f)

is a homomorphism of rings. An integral notation is often used for 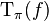\operatorname{T}_\pi(f), as in

\operatorname{T}_\pi(f)=\int_X f(x) d \pi(x) = \int_X f d \pi.

The theorem is also correct for unbounded measurable functions f, but then 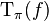\operatorname{T}_\pi(f) will be an unbounded linear operator on the Hilbert space H.

The spectral theorem says that every self-adjoint operator 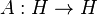A:H\to H has an associated projection-valued measure 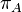\pi_A defined on the real axis, such that

A =\int_\mathbb{R} x d \pi_A(x).

This allows to define the Borel functional calculus for such operators: if 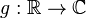g:\mathbb{R}\to\mathbb{C} is a measurable function, we set

g(A) :=\int_\mathbb{R} g(x) d \pi_A(x).

Structure of projection-valued measures

First we provide a general example of projection-valued measure based on direct integrals. Suppose (X, M, μ) is a measure space and let {Hx}x ∈ X be a μ-measurable family of separable Hilbert spaces. For every E ∈ M, let π(E) be the operator of multiplication by 1E on the Hilbert space

\int_X^\oplus H_x \ d \mu(x).

Then π is a projection-valued measure on (X, M).

Suppose π, ρ are projection-valued measures on (X, M) with values in the projections of H, K. π, ρ are unitarily equivalent if and only if there is a unitary operator U:H → K such that

\pi(E) = U^* \rho(E) U \quad

for every E ∈ M.

Theorem. If (X, M) is a standard Borel space, then for every projection-valued measure π on (X, M) taking values in the projections of a separable Hilbert space, there is a Borel measure μ and a μ-measurable family of Hilbert spaces {Hx}x ∈ X , such that π is unitarily equivalent to multiplication by 1E on the Hilbert space

\int_X^\oplus H_x \ d \mu(x).

The measure class of μ and the measure equivalence class of the multiplicity function x → dim Hx completely characterize the projection-valued measure up to unitary equivalence.

A projection-valued measure π is homogeneous of multiplicity n if and only if the multiplicity function has constant value n. Clearly,

Theorem. Any projection-valued measure π taking values in the projections of a separable Hilbert space is an orthogonal direct sum of homogeneous projection-valued measures:

\pi = \bigoplus_{1 \leq n \leq \omega} (\pi | H_n)

where

H_n = \int_{X_n}^\oplus H_x \ d (\mu | X_n) (x)

and

X_n = \{x \in X: \operatorname{dim} H_x = n\}.

Generalizations

The idea of a projection-valued measure is generalized by the positive operator-valued measure (POVM), where the need for the orthogonality implied by projection operators is replaced by the idea of a set of operators that are a non-orthogonal partition of unity. This generalization is motivated by applications to quantum information theory.

References