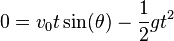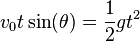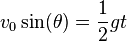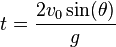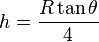Projectile motion

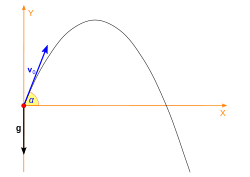
Projectile motion is a form of motion in which an object or particle (called a projectile) is thrown near the earth's surface, and it moves along a curved path under the action of gravity only. The only force of significance that acts on the object is gravity, which acts downward to cause a downward acceleration. There are no horizontal forces needed to maintain the horizontal motion – consistent with the concept of inertia.
The initial velocity
If the projectile is launched with an initial velocity 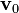 , then it can be written as
, then it can be written as
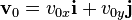 .
.
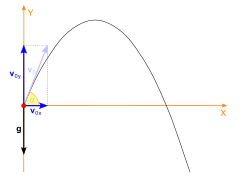
The components 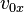 and
and 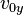 can be found if the angle,
can be found if the angle,  is known:
is known:
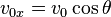 ,
,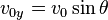 .
.
If the projectile's range, launch angle, and drop height are known, launch velocity can be found using Newton's formula
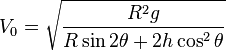 .
.
The launch angle is usually expressed by the symbol theta, but often the symbol alpha is used.
Kinematic quantities of projectile motion
In projectile motion, the horizontal motion and the vertical motion are independent of each other; that is, neither motion affects the other.
Acceleration
Since there is only acceleration in the vertical direction, the velocity in the horizontal direction is constant, being equal to 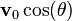 . The vertical motion of the projectile is the motion of a particle during its free fall. Here the acceleration is constant, being equal to
. The vertical motion of the projectile is the motion of a particle during its free fall. Here the acceleration is constant, being equal to  .[1] The components of the acceleration are:
.[1] The components of the acceleration are:
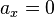 ,
,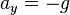 .
.
Velocity
The horizontal component of the velocity of the object remains unchanged throughout the motion. The vertical component of the velocity increases linearly, because the acceleration due to gravity is constant. The accelerations in the  and
and  directions can be integrated to solve for the components of velocity at any time
directions can be integrated to solve for the components of velocity at any time  , as follows:
, as follows:
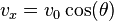 ,
,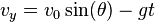 .
.
The magnitude of the velocity (under the Pythagorean theorem):
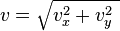 .
.
Displacement
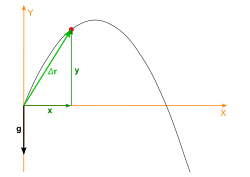
At any time  , the projectile's horizontal and vertical displacement:
, the projectile's horizontal and vertical displacement:
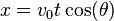 ,
,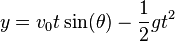 .
.
The magnitude of the displacement:
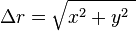 .
.
Parabolic trajectory
Consider the equations,
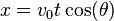 ,
,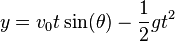 .
.
If t is eliminated between these two equations the following equation is obtained:
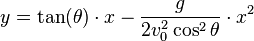 ,
,
This equation is the equation of a parabola.
Since  ,
,  , and
, and 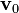 are constants, the above equation is of the form
are constants, the above equation is of the form
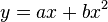 ,
,
in which  and
and  are constants. This is the equation of a parabola, so the path is parabolic. The axis of the parabola is vertical.
are constants. This is the equation of a parabola, so the path is parabolic. The axis of the parabola is vertical.
Time of Flight
The total time for which the projectile remains in the air is called the time of flight.
After the flight, the projectile returns to the horizontal axis, so y=0
Note that we have neglected air resistance on the projectile.
The maximum height of projectile
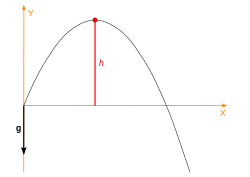
The highest height which the object will reach is known as the peak of the object's motion.
The increase of the height will last, until 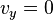 , that is,
, that is,
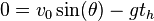 .
.
Time to reach the maximum height:
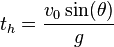 .
.
From the vertical displacement of the maximum height of projectile:
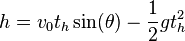
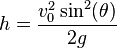 .
.
Relation during horizontal range and maximum height
The relation between the range  on the horizontal plane and the maximum height
on the horizontal plane and the maximum height 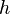 reached at
reached at 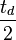 is:
is:
The maximum distance of projectile
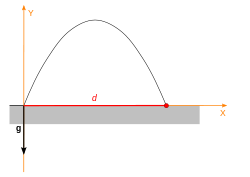
It is important to note that the Range and the Maximum height of the Projectile does not depend upon mass of the trajected body. Hence Range and Maximum height are equal for all those bodies which are thrown by same velocity and direction. Air resistance does not affect displacement of projectile.
The horizontal range d of the projectile is the horizontal distance the projectile has travelled when it returns to its initial height (y = 0).
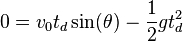 .
.
reach ground:
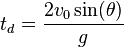 .
.
From the horizontal displacement the maximum distance of projectile:
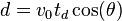 ,
,
so[2]
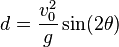 .
.
Note that  has its maximum value when
has its maximum value when
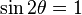 ,
,
which necessarily corresponds to
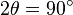 ,
,
or
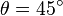 .
.
Application of the work energy theorem
According to the work-energy theorem the vertical component of velocity are listed below:
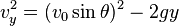 .
.
Projectile motion in art
- The sixth panel of Hwaseonghaenghaengdo Byeongpun (화성행행도 병풍) describes King Shooting Arrows at Deukjung Pavilion, 1795-02-14. According to palace records, Lady Hyegyeong, the King's mother, was so pleased to be presented with this 8-panels screen of such magnificent scale and stunning precision that she rewarded each of the seven artists who participated in its production. The artists were Choe Deuk-hyeon, Kim Deuk-sin, Yi Myeong-gyu, Jang Han-jong (1768 - 1815), Yun Seok-keun, Heo Sik (1762 - ?) and Yi In-mun.

득중정어사
Hwaseonghaenghaengdo Byeongpun
References
- Budó Ágoston: Kísérleti fizika I.,Budapest, Tankönyvkiadó, 1986. ISBN 963 17 8772 9 (Hungarian)
- Ifj. Zátonyi Sándor: Fizika 9.,Budapest, Nemzeti Tankönyvkiadó, 2009. ISBN 978-963-19-6082-2 (Hungarian)
- Hack Frigyes: Négyjegyű függvénytáblázatok, összefüggések és adatok, Budapest, Nemzeti Tankönyvkiadó, 2004. ISBN 963-19-3506-X (Hungarian)
Notes
- ↑ The
 is the acceleration due to gravity. (
is the acceleration due to gravity. (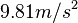 near the surface of the Earth).
near the surface of the Earth). - ↑
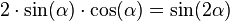
- Since the value of g is not specific the body with high velocity over g limit cannot be measured using the concept of the projectile motion