Productive efficiency
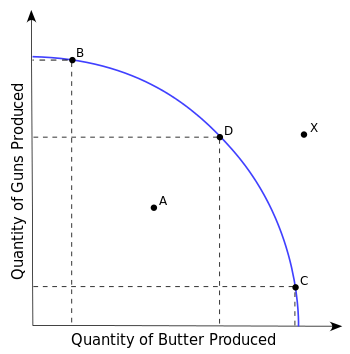

Productive efficiency occurs when the economy is using all of its resources efficiently. The concept is illustrated on a production possibility frontier (PPF) where all points on the curve are points of maximum productive efficiency (i.e., no more output can be achieved from the given inputs).[1] An equilibrium may be productively efficient without being allocatively efficient— i.e. it may result in a distribution of goods where social welfare is not maximized.
Productive efficiency occurs when production of one good is achieved at the lowest resource (input) cost possible, given the level of production of the other good(s). Equivalently, it occurs when the highest possible output of one good is produced, given the production level of the other good(s). In long-run equilibrium for perfectly competitive markets, this is at the base of the average total cost curve—i.e. where marginal cost equals average total cost.
Productive efficiency requires that all firms operate using best-practice technological and managerial processes. By improving these processes, an economy or business can extend its production possibility frontier outward, so that efficient production yields more output.
Due to the nature of monopolistic companies, they may not be productively efficient, because of X-inefficiency, whereby companies operating in a monopoly have less of an incentive to maximize output due to lack of competition. However, due to economies of scale it can be possible for the profit-maximizing level of output of monopolistic companies to occur with a lower price to the consumer than perfectly competitive companies.