Probability box
)%2Csteps%3D500.png)
A probability box (or p-box) is a characterization of an uncertain number consisting of both aleatoric and epistemic uncertainties that is often used in risk analysis or quantitative uncertainty modeling where numerical calculations must be performed. Probability bounds analysis is used to make arithmetic and logical calculations with p-boxes.
An example p-box is shown in the figure at right for an uncertain number x consisting of a left (upper) bound and a right (lower) bound on the probability distribution for x. The bounds are coincident for values of x below 0 and above 24. The bounds may have almost any shapes, including step functions, so long as they are monotonically increasing and do not cross each other. A p-box is used to express simultaneously incertitude (epistemic uncertainty), which is represented by the breadth between the left and right edges of the p-box, and variability (aleatory uncertainty), which is represented by the overall slant of the p-box.
Interpretation
_that_x_is_2.5_or_less.png)
.png)
There are dual interpretations of a p-box. It can be understood as bounds on the cumulative probability associated with any x-value. For instance, in the p-box depicted at right, the probability that the value will be 2.5 or less is between 4% and 36%. A p-box can also be understood as bounds on the x-value at any particular probability level. In the example, the 95th percentile is sure to be between 9 and 16.
If the left and right bounds of a p-box are sure to enclose the unknown distribution, the bounds are said to be rigorous, or absolute. The bounds may also be the tightest possible such bounds on the distribution function given the available information about it, in which case the bounds are therefore said to be best-possible. It may commonly be the case, however, that not every distribution that lies within these bounds is a possible distribution for the uncertain number, even when the bounds are rigorous and best-possible.
Mathematical definition
P-boxes are specified by left and right bounds on the cumulative probability distribution function (or, equivalently, the survival function) of a quantity and, optionally, additional information about the quantity’s mean, variance and distributional shape (family, unimodality, symmetry, etc.). A p-box represents a class of probability distributions consistent with these constraints.
Let 𝔻 denote the space of distribution functions on the real numbers ℝ, i.e., 𝔻 = {D | D : ℝ → [0,1], D(x) ≤ D(y) whenever x < y, for all x, y ∈ ℝ}, and let 𝕀 denote the set of real intervals, i.e., 𝕀 = {i | i = [i1, i2], i1 ≤ i2, i1, i2 ∈ ℝ}. Then a p-box is a quintuple {F, F, m, v, F}, where F, F ∈ 𝔻, while m, v ∈ 𝕀, and F ⊆ 𝔻. This quintuple denotes the set of distribution functions F ∈ 𝔻 matching the following constraints:
Thus, the constraints are that the distribution function F falls within prescribed bounds, the mean of the distribution (given by the Riemann-Stieltjes integral) is in the interval m, the variance of the distribution is in the interval v, and the distribution is within some admissible class of distributions F. The Riemann–Stieltjes integrals do not depend on the differentiability of F.
P-boxes serve the same role for random variables that upper and lower probabilities serve for events. In robust Bayes analysis[1] a p-box is also known as a distribution band.[2][3] A p-box can be constructed as a closed neighborhood of a distribution F ∈ 𝔻 under the Kolmogorov, Lévy or Wasserstein metric. A p-box is a crude but computationally convenient kind of credal set. Whereas a credal set is defined solely in terms of the constraint F as a convex set of distributions (which automatically determine F, F, m, and v, but are often very difficult to compute with), a p-box usually has a loosely constraining specification of F, or even no constraint so that F = 𝔻. Calculations with p-boxes, unlike credal sets, are often quite efficient, and algorithms for all standard mathematical functions are known.
A p-box is minimally specified by its left and right bounds, in which case the other constraints are understood to be vacuous as {F, F, [– 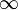 ,
, 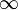 ], [0,
], [0, 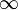 ], 𝔻}. Even when these ancillary constraints are vacuous, there may still be nontrivial bounds on the mean and variance that can be inferred from the left and right edges of the p-box.
], 𝔻}. Even when these ancillary constraints are vacuous, there may still be nontrivial bounds on the mean and variance that can be inferred from the left and right edges of the p-box.
Where p-boxes come from
P-boxes may arise from a variety of kinds of incomplete information about a quantity, and there are several ways to obtain p-boxes from data and analytical judgment.
Distributional p-boxes
When a probability distribution is known to have a particular shape (e.g., normal, uniform, beta, Weibull, etc.) but its parameters can only be specified imprecisely as intervals, the result is called a distributional p-box, or sometimes a parametric p-box. Such a p-box is usually easy to obtain by enveloping extreme distributions given the possible parameters. For instance, if a quantity is known to be normal with mean somewhere in the interval [7,8] and standard deviation within the interval [1,2], the left and right edges of the p-box can be found by enveloping the distribution functions of four probability distributions, namely, normal(7,1), normal(8,1), normal(7,2), and normal(8,2), where normal(μ,σ) represents a normal distribution with mean μ and standard deviation σ. All probability distributions that are normal and have means and standard deviations inside these respective intervals will have distribution functions that fall entirely within this p-box. The left and right bounds enclose many non-normal distributions, but these would be excluded from the p-box by specifying normality as the distribution family.
Distribution-free p-boxes
Even if the parameters such as mean and variance of a distribution are known precisely, the distribution cannot be specified precisely if the distribution family is unknown. In such situations, envelopes of all distributions matching given moments can be constructed from inequalities such as those due to Markov, Chebyshev, Cantelli, or Rowe[4][5] that enclose all distribution functions having specified parameters. These define distribution-free p-boxes because they make no assumption whatever about the family or shape of the uncertain distribution. When qualitative information is available, such as that the distribution is unimodal, the p-boxes can often be tightened substantially.[6]
P-boxes from imprecise measurements
When all members of a population can be measured, or when random sample data are abundant, analysts often use an empirical distribution to summarize the values. When those data have non-negligible measurement uncertainty represented by interval ranges about each sample value, an empirical distribution may be generalized to a p-box.[7] Such a p-box can be specified by cumulating the lower endpoints of all the interval measurements into a cumulative distribution forming the left edge of the p-box, and cumulating the upper endpoints to form the right edge. The broader the measurement uncertainty, the wider the resulting p-box.
Interval measurements can also be used to generalize distributional estimates based on the method of matching moments or maximum likelihood, that make shape assumptions such as normality or lognormality, etc.[7][8] Although the measurement uncertainty can be treated rigorously, the resulting distributional p-box generally will not be rigorous when it is a sample estimate based on only a subsample of the possible values. But, because these calculations take account of the dependence between the parameters of the distribution, they will often yield tighter p-boxes than could be obtained by treating the interval estimates of the parameters as unrelated as is done for distributional p-boxes.
Confidence bands
There may be uncertainty about the shape of a probability distribution because the sample size of the empirical data characterizing it is small. Several methods in traditional statistics have been proposed to account for this sampling uncertainty about the distribution shape, including Kolmogorov–Smirnov[9] and similar[10] confidence bands, which are distribution-free in the sense that they make no assumption about the shape of the underlying distribution. There are related confidence-band methods that do make assumptions about the shape or family of the underlying distribution, which can often result in tighter confidence bands.[11][12][13] Constructing confidence bands requires one to select the probability defining the confidence level, which usually must be less than 100% for the result to be non-vacuous. Confidence bands at the (1 − α)% confidence level are defined such that, (1 − α)% of the time they are constructed, they will completely enclose the distribution from which the data were randomly sampled. A confidence band about a distribution function is sometimes used as a p-box even though it represents statistical rather than rigorous or sure bounds. This use implicitly assumes that the true distribution, whatever it is, is inside the p-box.
An analogous Bayesian structure is called a Bayesian p-box,[14] which encloses all distributions having parameters within a subset of parameter space corresponding to some specified probability level from a Bayesian analysis of the data. This subset is the credible region for the parameters given the data, which could be defined as the highest posterior probability density region, or the lowest posterior loss region, or in some other suitable way. To construct a Bayesian p-box one must select a prior distribution, in addition to specifying the credibility level (analogous to a confidence level).
Envelopes of possible distributions
When there are multiple possible probability distributions that might describe a variable, and an analyst cannot discount any of them based on available information, a p-box can be constructed as the envelope of the various cumulative distributions.[15][16] It is also possible to account for the uncertainty about which distribution is the correct one with a sensitivity study, but such studies become more complex as the number of possible distributions grows, and combinatorially more complex as the number of variables about which there could be multiple distributions increases. An enveloping approach is more conservative about this uncertainty than various alternative approaches to handle the uncertainty which average together distributions in stochastic mixture models or Bayesian model averages. The unknown true distribution is likely to be within the class of distributions encompassed by the p-box. In contrast, assuming the true distribution is one of the distributions being averaged, the average distribution is sure to be unlike the unknown true distribution.
P-boxes from calculation results
P-boxes can arise from computations involving probability distributions, or involving both a probability distribution and an interval, or involving other p-boxes. For example, the sum of a quantity represented by a probability distribution and a quantity represented by an interval will generally be characterized by a p-box.[17] The sum of two random variables characterized by well-specified probability distributions is another precise probability distribution typically only when the copula (dependence function) between the two summands is completely specified. When their dependence is unknown or only partially specified, the sum will be more appropriately represented by a p-box because different dependence relations lead to many different distributions for the sum. Kolmogorov originally asked what bounds could be placed about the distribution of a sum when nothing is known about the dependence between the distributions of the addends.[18] The question was only answered in the early 1980s. Since that time, formulas and algorithms for sums have been generalized and extended to differences, products, quotients and other binary and unary functions under various dependence assumptions.[18][19][20][21][22][23][24]
These methods, collectively called probability bounds analysis, provide algorithms to evaluate mathematical expressions when there is uncertainty about the input values, their dependencies, or even the form of mathematical expression itself. The calculations yield results that are guaranteed to enclose all possible distributions of the output variable if the input p-boxes were also sure to enclose their respective distributions. In some cases, a calculated p-box will also be best-possible in the sense that only possible distributions are within the p-box, but this is not always guaranteed. For instance, the set of probability distributions that could result from adding random values without the independence assumption from two (precise) distributions is generally a proper subset of all the distributions admitted by the computed p-box. That is, there are distributions within the output p-box that could not arise under any dependence between the two input distributions. The output p-box will, however, always contain all distributions that are possible, so long as the input p-boxes were sure to enclose their respective underlying distributions. This property often suffices for use in risk analysis.
Special cases
Precise probability distributions and intervals are special cases of p-boxes, as are real values and integers. Because a probability distribution expresses variability and lacks incertitude, the left and right bounds of its p-box are coincident for all x-values at the value of the cumulative distribution function (which is a non-decreasing function from zero to one). Mathematically, a probability distribution F is the degenerate p-box {F, F, E(F), V(F), F}, where E and V denote the expectation and variance operators. An interval expresses only incertitude. Its p-box looks like a rectangular box whose upper and lower bounds jump from zero to one at the endpoints of the interval. Mathematically, an interval [a, b] corresponds to the degenerate p-box {H(a), H(b), [a, b], [0, (b–a)2/4], 𝔻}, where H denotes the Heaviside step function. A precise scalar number c lacks both kinds of uncertainty. Its p-box is just a step function from 0 to 1 at the value c; mathematically this is {H(c), H(c), c, 0, H(c)}.
Applications
P-boxes and probability bounds analysis have been used in many applications spanning many disciplines in engineering and environmental science, including:
- Engineering design[25]
- Expert elicitation[26]
- Analysis of species sensitivity distributions[27]
- Sensitivity analysis in aerospace engineering of the buckling load of the frontskirt of the Ariane 5 launcher[28]
- ODE models of chemical reactor dynamics[29][30]
- Pharmacokinetic variability of inhaled VOCs[31]
- Groundwater modeling[32]
- Bounding failure probability for series systems[33]
- Heavy metal contamination in soil at an ironworks brownfield[34][35]
- Uncertainty propagation for salinity risk models[36]
- Power supply system safety assessment[37]
- Contaminated land risk assessment[38]
- Engineered systems for drinking water treatment[39]
- Computing soil screening levels[40]
- Human health and ecological risk analysis by the U.S. EPA of PCB contamination at the Housatonic River Superfund site[41]
- Environmental assessment for the Calcasieu Estuary Superfund site[42]
- Aerospace engineering for supersonic nozzle thrust[43]
- Verification and validation in scientific computation for engineering problems[44]
- Toxicity to small mammals of environmental mercury contamination[45]
- Modeling travel time of pollution in groundwater[46]
- Reliability analysis[47]
- Endangered species assessment for reintroduction of Leadbeater’s Possum[48]
- Exposure of insectivorous birds to an agricultural pesticide[49]
- Climate change projections[34][50][51]
- Waiting time in queuing systems[52]
- Extinction risk analysis for spotted owl on the Olympic Peninsula[53]
- Biosecurity against introduction of invasive species or agricultural pests[54]
- Finite-element structural analysis[55][56]
- Cost estimates[57]
- Nuclear stockpile certification[58]
- Fracking risks to water pollution[59]
Criticisms
No internal structure. Because a p-box retains little information about any internal structure within the bounds, it does not elucidate which distributions within the p-box are most likely, nor whether the edges represent very unlikely or distinctly likely scenarios. This could complicate decisions in some cases if an edge of a p-box encloses a decision threshold.
Loses information. To achieve computational efficiency, p-boxes lose information compared to more complex Dempster-Shafer structures or credal sets.[15] In particular, p-boxes lose information about the mode (most probable value) of a quantity. This information could be useful to keep, especially in situations where the quantity is an unknown but fixed value.
Traditional probability sufficient. Some critics of p-boxes argue that precisely specified probability distributions are sufficient to characterize uncertainty of all kinds. For instance, Lindley has asserted, "Whatever way uncertainty is approached, probability is the only sound way to think about it."[60][61] These critics argue that it is meaningless to talk about ‘uncertainty about probability’ and that traditional probability is a complete theory that is sufficient to characterize all forms of uncertainty. Under this criticism, users of p-boxes have simply not made the requisite effort to identify the appropriate precisely specified distribution functions.
Possibility theory can do better. Some critics contend that it makes sense in some cases to work with a possibility distribution rather than working separately with the left and right edges of p-boxes. They argue that the set of probability distributions induced by a possibility distribution is a subset of those enclosed by an analogous p-box's edges.[62][63] Others make a counterargument that one cannot do better with a possibility distribution than with a p-box.[64]
See also
- uncertain number
- interval
- cumulative probability distribution
- upper and lower probabilities
- credal set
- risk analysis
- uncertainty propagation
- probability bounds analysis
- Dempster–Shafer theory and the section on Dempster–Shafer structure
- imprecise probability
- simultaneous confidence bands on distribution and survival functions using likelihood ratios[13]
- pointwise binomial confidence intervals for F(X) for a given X[65]
- uncertainty propagation software
References
- ↑ Berger, J.O. (1984). The robust Bayesian viewpoint. Pages 63–144 in Robustness of Bayesian analyses, edited by J.B. Kadane, Elsevier Science.
- ↑ Basu, S. (1994). Variations of posterior expectations for symmetric unimodal priors in a distribution band. Sankhyā: The Indian Journal of Statistics, Series A 56: 320–334.
- ↑ Basu, S., and A. DasGupta (1995). Robust Bayesian analysis with distribution bands. Statistics and Decisions 13: 333–349.
- ↑ Rowe, N.C. (1988). Absolute bounds on the mean and standard deviation of transformed data for constant-sign-derivative transformations. SIAM Journal of Scientific and Statistical Computing 9: 1098–1113.
- ↑ Smith, J.E. (1995). Generalized Chebychev inequalities: theory and applications in decision analysis. Operations Research 43: 807–825.
- ↑ Zhang, J. and D. Berleant (2005). Arithmetic on random variables: squeezing the envelopes with new joint distribution constraints. Pages 416–422 in Proceedings of the Fourth International Symposium On Imprecise Probabilities and Their Applications (ISIPTA ’05), Carnegie Mellon University, Pittsburgh, July 20–23, 2005.
- ↑ 7.0 7.1 Ferson, S., V. Kreinovich, J. Hajagos, W. Oberkampf, and L. Ginzburg (2007). Experimental Uncertainty Estimation and Statistics for Data Having Interval Uncertainty. Sandia National Laboratories, SAND 2007-0939, Albuquerque, NM.
- ↑ Xiang, G., V. Kreinovich and S. Ferson, (2007). Fitting a normal distribution to interval and fuzzy data. Pages 560–565 in Proceedings of the 26th International Conference of the North American Fuzzy Information Processing Society NAFIPS'2007, M. Reformat and M.R. Berthold (eds.).
- ↑ Kolmogorov, A. (1941). Confidence Limits for an Unknown Distribution Function. Annals of Mathematical Statistics 12: 461–463.
- ↑ Owen, A.B. (1995). Nonparametric likelihood confidence bands for a distribution function. Journal of the American Statistical Association 90: 516–521.
- ↑ Cheng, R.C.H., and T.C. Iles (1983). Confidence bands for cumulative distribution functions of continuous random variables. Technometrics 25: 77–86.
- ↑ Cheng, R.C.H., B.E. Evans and J.E. Williams (1988). Confidence band estimations for distributions used in probabilistic design. International Journal of Mechanical Sciences 30: 835–845.
- ↑ 13.0 13.1 Murphy, S.A. (1995). Likelihood ratio-based confidence intervals in survival analysis. Journal of the American Statistical Association 90: 1399–1405.
- ↑ Montgomery, V. (2009). New Statistical Methods in Risk Assessment by Probability Bounds. Ph.D. dissertation, Durham University, UK.
- ↑ 15.0 15.1 Ferson, S., V. Kreinovich, L. Ginzburg, D.S. Myers, and K. Sentz (2003). Constructing Probability Boxes and Dempster–Shafer Structures. Sandia National Laboratories, SAND2002-4015, Albuquerque, NM.
- ↑ Fu, G., D. Butler, S.-T. Khu, and S. Sun (2011). Imprecise probabilistic evaluation of sewer flooding in urban drainage systems using random set theory. Water Resources Research 47: W02534.
- ↑ Ferson, S., and L.R. Ginzburg (1996). Different methods are needed to propagate ignorance and variability. Reliability Engineering and Systems Safety 54: 133–144.
- ↑ 18.0 18.1 Frank, M.J., R.B. Nelsen and B. Schweizer (1987). Best-possible bounds for the distribution of a sum—a problem of Kolmogorov. Probability Theory and Related Fields 74: 199–211.
- ↑ Yager, R.R. (1986). Arithmetic and other operations on Dempster–Shafer structures. International Journal of Man-machine Studies 25: 357–366.
- ↑ Williamson, R.C., and T. Downs (1990). Probabilistic arithmetic I: Numerical methods for calculating convolutions and dependency bounds. International Journal of Approximate Reasoning 4: 89–158.
- ↑ Berleant, D. (1993). Automatically verified reasoning with both intervals and probability density functions. Interval Computations 1993 (2) : 48–70.
- ↑ Berleant, D., G. Anderson, and C. Goodman-Strauss (2008). Arithmetic on bounded families of distributions: a DEnv algorithm tutorial. Pages 183–210 in Knowledge Processing with Interval and Soft Computing, edited by C. Hu, R.B. Kearfott, A. de Korvin and V. Kreinovich, Springer (ISBN 978-1-84800-325-5).
- ↑ Berleant, D., and C. Goodman-Strauss (1998). Bounding the results of arithmetic operations on random variables of unknown dependency using intervals. Reliable Computing 4: 147–165.
- ↑ Ferson, S., R. Nelsen, J. Hajagos, D. Berleant, J. Zhang, W.T. Tucker, L. Ginzburg and W.L. Oberkampf (2004). Dependence in Probabilistic Modeling, Dempster–Shafer Theory, and Probability Bounds Analysis. Sandia National Laboratories, SAND2004-3072, Albuquerque, NM.
- ↑ Aughenbaugh, J. M., and C.J.J. Paredis (2007). Probability bounds analysis as a general approach to sensitivity analysis in decision making under uncertainty. SAE 2007 Transactions Journal of Passenger Cars: Mechanical Systems, (Section 6) 116: 1325–1339, SAE International, Warrendale, Pennsylvania.
- ↑ Flander, L., W. Dixon, M. McBride, and M. Burgman. (2012). Facilitated expert judgment of environmental risks: acquiring and analysing imprecise data. International Journal of Risk Assessment and Management 16: 199–212.
- ↑ Dixon, W.J. (2007). The use of Probability Bounds Analysis for Characterising and Propagating Uncertainty in Species Sensitivity Distributions. Technical Report Series No. 163, Arthur Rylah Institute for Environmental Research, Department of Sustainability and Environment. Heidelberg, Victoria, Australia.
- ↑ Oberguggenberger, M., J. King and B. Schmelzer (2007). Imprecise probability methods for sensitivity analysis in engineering. Proceedings of the 5th International Symposium on Imprecise Probability: Theories and Applications, Prague, Czech Republic.
- ↑ Enszer, J.A., Y. Lin, S. Ferson, G.F. Corliss and M.A. Stadtherr (2011). Probability bounds analysis for nonlinear dynamic process models. AIChE Journal 57: 404–422.
- ↑ Enszer, Joshua Alan, (2010). Verified Probability Bound Analysis for Dynamic Nonlinear Systems. Dissertation, University of Notre Dame.
- ↑ Nong, A., and K. Krishnan (2007). Estimation of interindividual pharmacokinetic variability factor for inhaled volatile organic chemicals using a probability-bounds approach. Regulatory Toxicology and Pharmacology 48: 93–101.
- ↑ Guyonnet, D., F. Blanchard, C. Harpet, Y. Ménard, B. Côme and C. Baudrit (2005). Projet IREA—Traitement des incertitudes en évaluation des risques d'exposition, Annexe B, Cas «Eaux souterraines». Rapport BRGM/RP-54099-FR, Bureau de Recherches Géologiques et Minières, France.
- ↑ Fetz, T., and F. Tonon (2008). Probability bounds for series systems with variables constrained by sets of probability measures. International Journal of Reliability and Safety 2: 309–339. doi:10.1504/IJRS.2008.022079.
- ↑ 34.0 34.1 Augustsson, A., M. Filipsson, T. Öberg, B. Bergbäck (2011). Climate change—an uncertainty factor in risk analysis of contaminated land. Science of the Total Environment 409: 4693–4700.
- ↑ Baudrit, C., D. Guyonnet, H. Baroudi, S. Denys and P. Begassat (2005). Assessment of child exposure to lead on an ironworks brownfield: uncertainty analysis. 9th International FZK/TNO Conference on Contaminated Soil – ConSoil2005, Bordeaux, France, pages 1071–1080.
- ↑ Dixon, W.J. (2007). Uncertainty Propagation in Population Level Salinity Risk Models. Technical Report Technical Report Series No. 164, Arthur Rylah Institute for Environmental Research. Heidelberg, Victoria, Australia
- ↑ Karanki, D.R., H.S. Kushwaha, A.K. Verma, and S. Ajit. (2009). Uncertainty analysis based on probability bounds (p-box) approach in probabilistic safety assessment. Risk Analysis 29: 662–75.
- ↑ Sander, P., B. Bergbäck and T. Öberg (2006). Uncertain numbers and uncertainty in the selection of input distributions—Consequences for a probabilistic risk assessment of contaminated land. Risk Analysis 26: 1363–1375.
- ↑ Minnery, J.G., J.G. Jacangelo, L.I. Boden, D.J. Vorhees and W. Heiger-Bernays (2009). Sensitivity analysis of the pressure-based direct integrity test for membranes used in drinking water treatment. Environmental Science and Technology 43(24): 9419–9424.
- ↑ Regan, H.M., B.E. Sample and S. Ferson (2002). Comparison of deterministic and probabilistic calculation of ecological soil screening levels. Environmental Toxicology and Chemistry 21: 882–890.
- ↑ U.S. Environmental Protection Agency (Region I), GE/Housatonic River Site in New England
- ↑ U.S. Environmental Protection Agency (Region 6 Superfund Program), Calcasieu Estuary Remedial Investigation
- ↑ Roy, C.J., and M.S. Balch (2012). A holistic approach to uncertainty quantification with application to supersonic nozzle thrust. International Journal for Uncertainty Quantification 2: 363-381. doi:10.1615/Int.J.UncertaintyQuantification.2012003562.
- ↑ Oberkampf, W.L., and C. J. Roy. (2010). Verification and Validation in Scientific Computing. Cambridge University Press.
- ↑ Regan, H.M., B.K. Hope, and S. Ferson (2002). Analysis and portrayal of uncertainty in a food web exposure model. Human and Ecological Risk Assessment 8: 1757–1777.
- ↑ Ferson, S., and W.T. Tucker (2004). Reliability of risk analyses for contaminated groundwater. Groundwater Quality Modeling and Management under Uncertainty, edited by S. Mishra, American Society of Civil Engineers Reston, VA.
- ↑ Crespo, L.G., S.P. Kenny, and D.P. Giesy (2012). Reliability analysis of polynomial systems subject to p-box uncertainties. Mechanical Systems and Signal Processing 37: 121–136. doi:10.1016/j.ymssp.2012.08.012
- ↑ Ferson, S., and M. Burgman (1995). Correlations, dependency bounds and extinction risks. Biological Conservation 73: 101–105.
- ↑ Ferson, S., D.R.J. Moore, P.J. Van den Brink, T.L. Estes, K. Gallagher, R. O'Connor and F. Verdonck. (2010). Bounding uncertainty analyses. Pages 89–122 in Application of Uncertainty Analysis to Ecological Risks of Pesticides, edited by W. J. Warren-Hicks and A. Hart. CRC Press, Boca Raton, Florida.
- ↑ Kriegler, E., and H. Held (2005). Utilizing belief functions for the estimation of future climate change. International Journal of Approximate Reasoning 39: 185–209.
- ↑ Kriegler, E. (2005). Imprecise probability analysis for integrated assessment of climate change, Ph.D. dissertation, Universität Potsdam, Germany.
- ↑ Batarseh, O.G.Y., (2010). An Interval Based Approach to Model Input Uncertainty in Discrete-event Simulation. Ph.D. dissertation, University of Central Florida.
- ↑ Goldwasser, L., L. Ginzburg and S. Ferson (2000). Variability and measurement error in extinction risk analysis: the northern spotted owl on the Olympic Peninsula. Pages 169–187 in Quantitative Methods for Conservation Biology, edited by S. Ferson and M. Burgman, Springer-Verlag, New York.
- ↑ Hayes, K.R. (2011). Uncertainty and uncertainty analysis methods: Issues in quantitative and qualitative risk modeling with application to import risk assessment ACERA project (0705). Report Number: EP102467, CSIRO, Hobart, Australia.
- ↑ Zhang, H., R.L. Mullen, and R.L. Muhanna (2010). Finite element structural analysis using imprecise probabilities based on p-box representation. Proceedings of the 4th International Workshop on Reliable Engineering Computing (REC 2010).
- ↑ Zhang, H., R. Mullen, R. Muhanna (2012). Safety Structural Analysis with Probability-Boxes. International Journal of Reliability and Safety 6: 110–129.
- ↑ Mehl, C.H. (2013). P-boxes for cost uncertainty analysis. Mechanical Systems and Signal Processing 37: 253–263. doi:10.1016/j.ymssp.2012.03.014
- ↑ Sentz, K., and S. Ferson (2011). Probabilistic bounding analysis in the quantification of margins and uncertainties. Reliability Engineering and System Safety 96: 1126–1136.
- ↑ Rozell, Daniel J., and Sheldon J. Reaven (2012). Water pollution risk associated with natural gas extraction from the Marcellus Shale. Risk Analysis 32: 1382–1393.
- ↑ Page 71 in Lindley, D.V. (2006). Understanding Uncertainty. John Wiley & Sons, Hoboken, New Jersey.
- ↑ http://en.wikiquote.org/wiki/Dennis_Lindley
- ↑ Baudrit, C., D. Dubois, H. Fargier (2003). Représentation de la connaissance probabiliste incomplète. Pages 65–72 in Actes Rencontres Francophones sur la Logique Floue et ses Applications (LFA'03), Tours, France. Cépaduès-Éditions.
- ↑ Baudrit, C. (2005.) Représentation et propagation de connaissances imprécises et incertaines : Application à l'évaluation des risques liés aux sites et aux sols pollués. Ph.D. dissertation, Université Paul Sabatier, Toulouse III.
- ↑ Troffaes, M.C.M., and S. Destercke (2011). Probability boxes on totally preordered spaces for multivariate modelling. International Journal of Approximate Reasoning (in press).
- ↑ Meeker, W.Q., and L.A. Escobar (1998). Statistical Methods for Reliability Data, John Wiley and Sons, New York.
Additional references
- Baudrit, C., and D. Dubois (2006). Practical representations of incomplete probabilistic knowledge. Computational Statistics & Data Analysis 51: 86–108.
- Baudrit, C., D. Dubois, D. Guyonnet (2006). Joint propagation and exploitation of probabilistic and possibilistic information in risk assessment. IEEE Transactions on Fuzzy Systems 14: 593–608.
- Bernardini, A., and F. Tonon (2009). Extreme probability distributions of random/fuzzy sets and p-boxes. International Journal of Reliability and Safety 3: 57-78. (alternative link)
- Destercke, S., D. Dubois and E. Chojnacki (2008). Unifying practical uncertainty representations – I: Generalized p-boxes. International Journal of Approximate Reasoning 49: 649–663 .
- Dubois, D. (2010). (Commentary) Representation, propagation, and decision issues in risk analysis under incomplete probabilistic information. Risk Analysis 30: 361–368. doi:10.1111/j.1539-6924.2010.01359.x.
- Dubois, D., and D. Guyonnet (2011). Risk-informed decision-making in the presence of epistemic uncertainty. International Journal of General Systems 40: 145–167.
- Guyonnet, D., F. Blanchard, C. Harpet, Y. Ménard, B. Côme and C. Baudrit (2005). Projet IREA—Traitement des incertitudes en évaluation des risques d'exposition. Rapport BRGM/RP-54099-FR, Bureau de Recherches Géologiques et Minières, France.