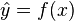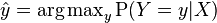Probabilistic classification

Machine learning and data mining

Problems
Classification Clustering Regression Anomaly detection Association rules Reinforcement learning Structured prediction Feature learning Online learning Semi-supervised learning Grammar induction
Supervised learning (classification • regression)
Decision trees Ensembles (Bagging, Boosting, Random forest) k-NN Linear regression Naive Bayes Neural networks Logistic regression Perceptron Support vector machine (SVM) Relevance vector machine (RVM)
Clustering
BIRCH Hierarchical k-means Expectation-maximization (EM) DBSCAN OPTICS Mean-shift
Dimensionality reduction
Factor analysis CCA ICA LDA NMF PCA t-SNE
Structured prediction
Graphical models (Bayes net, CRF, HMM)
Anomaly detection
k-NN Local outlier factor
Neural nets
Autoencoder Deep learning Multilayer perceptron RNN Restricted Boltzmann machine SOM Convolutional neural network
Theory
Bias-variance dilemma Computational learning theory Empirical risk minimization PAC learning Statistical learning VC theory
Machine learning portal Computer science portal Statistics portal

In machine learning, a probabilistic classifier is a classifier that is able to predict, given a sample input, a probability distribution over a set of classes, rather than only outputting the most likely class that the sample should belong to. Probabilistic classifiers provide classification with a degree of certainty, which can be useful in its own right,^[1] or when combining classifiers into ensembles.

Formally, an "ordinary" classifier is some rule, or function, that assigns to a sample $x$ a class label $ŷ$ :

\hat{y} = f(x)

The samples come from some set $X$ (e.g., the set of all documents, or the set of all images), while the class labels form a finite set $Y$ defined prior to training.

Probabilistic classifiers generalize this notion of classifiers: instead of functions, they are conditional distributions 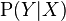$\operatorname{P}(Y \vert X)$ , meaning that for a given 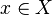$x \in X$ , they assign probabilities to all 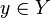$y \in Y$ (and these probabilities sum to one). "Hard" classification can then be done using the optimal decision rule^[2]^:39–40

\hat{y} = \operatorname{\arg\max}_{y} \operatorname{P}(Y=y \vert X)

Binary probabilistic classifiers are also called binomial regression models in statistics. In econometrics, probabilistic classification in general is called discrete choice.

Some classification models, such as naive Bayes, logistic regression and multilayer perceptrons (when trained under an appropriate loss function) are naturally probabilistic. Other models such as support vector machines are not, but methods exist to turn them into probabilistic classifiers.

Generative and conditional training

Some models, such as logistic regression, are conditionally trained: they optimize the conditional probability 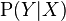$\operatorname{P}(Y \vert X)$ directly on a training set (see empirical risk minimization). Other classifiers, such as naive Bayes, are trained generatively: at training time, the class-conditional distribution 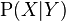$\operatorname{P}(X \vert Y)$ and the class prior 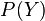$P(Y)$ are found, and the conditional distribution 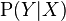$\operatorname{P}(Y \vert X)$ is derived using Bayes' rule.^[2]^:43

Probability calibration

Not all classification models are naturally probabilistic, and some that are, notably naive Bayes classifiers and boosting methods, produce distorted class probability distributions.^[3] However, for classification models that produce some kind of "score" on their outputs (such as a distorted probability distribution or the "signed distance to the hyperplane" in a support vector machine), there are several methods that turn these scores into properly calibrated class membership probabilities.

For the binary case, a common approach is to apply Platt scaling, which learns a logistic regression model on the scores.^[4] An alternative method using isotonic regression^[5] is generally superior to Platt's method when sufficient training data is available.^[3]

In the multiclass case, one can use a reduction to binary tasks, followed by univariate calibration with an algorithm as described above and further application of the pairwise coupling algorithm by Hastie and Tibshirani.^[6] An alternative one-step method, the Dirichlet calibration, is introduced by Gebel and Weihs.^[7]

Evaluating probabilistic classification

Commonly used loss functions for probabilistic classification include log loss and the mean squared error between the predicted and the true probability distributions. The former of these is commonly used to train logistic models.

References

↑ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). The Elements of Statistical Learning. p. 348. [I]n data mining applications the interest is often more in the class probabilities 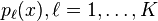$p_\ell(x), \ell = 1, \dots, K$ themselves, rather than in performing a class assignment.
↑ 2.0 2.1 Bishop, Christopher M. (2006). Pattern Recognition and Machine Learning. Springer.
↑ 3.0 3.1 Niculescu-Mizil, Alexandru; Caruana, Rich (2005). Predicting good probabilities with supervised learning (PDF). ICML. doi:10.1145/1102351.1102430.
↑ Platt, John (1999). "Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods" (PDF). Advances in large margin classifiers 10 (3): 61–74.
↑ Zadrozny, Bianca; Elkan, Charles (2002). "Transforming classifier scores into accurate multiclass probability estimates". Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '02 (PDF). pp. 694–699. doi:10.1145/775047.775151. ISBN 1-58113-567-X. CiteSeerX: 10.1.1.13.7457.
↑ Hastie, Trevor; Tibshirani, Robert (1998). "Classification by pairwise coupling". The Annals of Statistics 26 (2): 451–471. doi:10.1214/aos/1028144844. Zbl 0932.62071. CiteSeerX: 10.1.1.46.6032.
↑ Gebel, Martin; Weihs, Claus (2008). "Calibrating Margin-Based Classifier Scores into Polychotomous Probabilities". In Preisach, Christine; Burkhardt, Hans; Schmidt-Thieme, Lars; Decker, Reinhold. Data Analysis, Machine Learning and Applications. Studies in Classification, Data Analysis, and Knowledge Organization. pp. 29–36. doi:10.1007/978-3-540-78246-9_4. ISBN 978-3-540-78239-1.