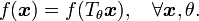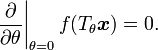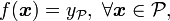Prior knowledge for pattern recognition

Pattern recognition is a very active field of research intimately bound to machine learning. Also known as classification or statistical classification, pattern recognition aims at building a classifier that can determine the class of an input pattern. This procedure, known as training, corresponds to learning an unknown decision function based only on a set of input-output pairs 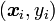$(\boldsymbol{x}_i,y_i)$ that form the training data (or training set). Nonetheless, in real world applications such as character recognition, a certain amount of information on the problem is usually known beforehand. The incorporation of this prior knowledge into the training is the key element that will allow an increase of performance in many applications.

Definition

Prior knowledge^[1] refers to all information about the problem available in addition to the training data. However, in this most general form, determining a model from a finite set of samples without prior knowledge is an ill-posed problem, in the sense that a unique model may not exist. Many classifiers incorporate the general smoothness assumption that a test pattern similar to one of the training samples tends to be assigned to the same class.

The importance of prior knowledge in machine learning is suggested by its role in search and optimization. Loosely, the no free lunch theorem states that all search algorithms have the same average performance over all problems, and thus implies that to gain in performance on a certain application one must use a specialized algorithm that includes some prior knowledge about the problem.

The different types of prior knowledge encountered in pattern recognition are now regrouped under two main categories: class-invariance and knowledge on the data.

Class-invariance

A very common type of prior knowledge in pattern recognition is the invariance of the class (or the output of the classifier) to a transformation of the input pattern. This type of knowledge is referred to as transformation-invariance. The mostly used transformations used in image recognition are:

Incorporating the invariance to a transformation 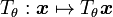$T_{\theta}: \boldsymbol{x} \mapsto T_{\theta}\boldsymbol{x}$ parametrized in $\theta$ into a classifier of output 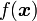$f(\boldsymbol{x})$ for an input pattern 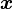$\boldsymbol{x}$ corresponds to enforcing the equality

f(\boldsymbol{x}) = f(T_{\theta}\boldsymbol{x}), \quad \forall \boldsymbol{x}, \theta .

Local invariance can also be considered for a transformation centered at 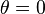$\theta=0$ , so that 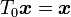$T_0\boldsymbol{x} = \boldsymbol{x}$ , by using the constraint

\left.\frac{\partial}{\partial \theta}\right|_{\theta=0} f(T_{\theta} \boldsymbol{x}) = 0 .

The function $f$ in these equations can be either the decision function of the classifier or its real-valued output.

Another approach is to consider class-invariance with respect to a "domain of the input space" instead of a transformation. In this case, the problem becomes finding $f$ so that

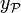f(\boldsymbol{x}) = y_{\mathcal{P}},\ \forall \boldsymbol{x}\in \mathcal{P} ,

where $y_{\mathcal{P}}$ is the membership class of the region 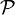$\mathcal{P}$ of the input space.

A different type of class-invariance found in pattern recognition is permutation-invariance, i.e. invariance of the class to a permutation of elements in a structured input. A typical application of this type of prior knowledge is a classifier invariant to permutations of rows of the matrix inputs.

Knowledge of the data

Other forms of prior knowledge than class-invariance concern the data more specifically and are thus of particular interest for real-world applications. The three particular cases that most often occur when gathering data are:

Unlabeled samples are available with supposed class-memberships;
Imbalance of the training set due to a high proportion of samples of a class;
Quality of the data may vary from a sample to another.

Prior knowledge of these can enhance the quality of the recognition if included in the learning. Moreover, not taking into account the poor quality of some data or a large imbalance between the classes can mislead the decision of a classifier.

Notes

↑ B. Scholkopf and A. Smola, "Learning with Kernels", MIT Press 2002.

References

E. Krupka and N. Tishby, "Incorporating Prior Knowledge on Features into Learning", Eleventh International Conference on Artificial Intelligence and Statistics (AISTATS 07)