Principalization (algebra)
In the mathematical field of algebraic number theory, the concept principalization has its origin in David Hilbert's 1897 conjecture that all ideals of an algebraic number field, which can always be generated by two algebraic numbers, become principal ideals, generated by a single algebraic number, when they are transferred to the maximal abelian unramified extension field, which was later called the Hilbert class field, of the given base field. More than thirty years later, Philipp Furtwängler succeeded in proving this principal ideal theorem in 1930, after it had been translated from number theory to group theory by E. Artin in 1929, who made use of his general reciprocity law to establish the reformulation. Since this long desired proof was achieved by means of Artin transfers of non-abelian groups with derived length two, several investigators tried to exploit the theory of such groups further to obtain additional information on the principalization in intermediate fields between the base field and its Hilbert class field. The first contributions in this direction are due to A. Scholz and O. Taussky in 1934, who coined the synonym capitulation for principalization. Another independent access to the principalization problem via Galois cohomology of unit groups is also due to Hilbert and goes back to the chapter on cyclic relative extensions of prime degree in his number report 1897, which culminates in the famous Theorem 94.
Extension of classes
Let  be an algebraic number field, called the base field, and let
be an algebraic number field, called the base field, and let 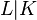 be a field extension of finite degree.
be a field extension of finite degree.
Definition.
The embedding monomorphism of fractional ideals 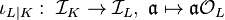 , where
, where 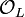 denotes the ring of integers of
denotes the ring of integers of 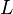 , induces the extension homomorphism of ideal classes
, induces the extension homomorphism of ideal classes
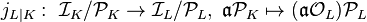 , where
, where 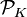 and
and 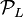 denote the subgroups of principal ideals.
denote the subgroups of principal ideals.
If there exists a non-principal ideal 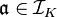 , with non trivial class
, with non trivial class 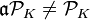 , whose extension ideal in
, whose extension ideal in 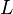 is principal,
is principal, 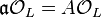 for some number
for some number 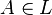 , and hence belongs to the trivial class
, and hence belongs to the trivial class 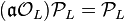 , then we speak about principalization or capitulation in
, then we speak about principalization or capitulation in 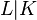 . In this case, the ideal
. In this case, the ideal 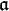 and its class
and its class 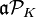 are said to principalize or capitulate in
are said to principalize or capitulate in 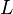 . This phenomenon is described most conveniently by the principalization kernel or capitulation kernel, that is the kernel
. This phenomenon is described most conveniently by the principalization kernel or capitulation kernel, that is the kernel 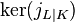 of the class extension homomorphism.
of the class extension homomorphism.
Remark.
When 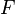 is a Galois extension of
is a Galois extension of  with automorphism group
with automorphism group 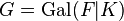 such that
such that 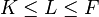 is an intermediate field with relative group
is an intermediate field with relative group 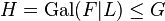 , more precise statements about the homomorphisms
, more precise statements about the homomorphisms 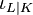 and
and 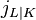 are possible by using group theory. According to the theories of A. Hurwitz 1895
[1]
and D. Hilbert 1897
[2]
on the decomposition of a prime ideal
are possible by using group theory. According to the theories of A. Hurwitz 1895
[1]
and D. Hilbert 1897
[2]
on the decomposition of a prime ideal 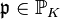 in the extension
in the extension 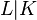 , viewed as a subextension of
, viewed as a subextension of 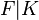 , we have
, we have 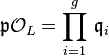 , where the
, where the 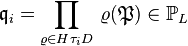 , with
, with 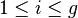 , are the prime ideals lying over
, are the prime ideals lying over 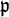 in
in 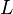 , expressed by a fixed prime ideal
, expressed by a fixed prime ideal 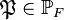 dividing
dividing 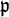 in
in 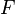 and a double coset decomposition
and a double coset decomposition 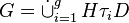 of
of  modulo
modulo 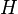 and modulo the decomposition group (stabilizer)
and modulo the decomposition group (stabilizer) 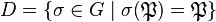 of
of 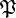 in
in  , with a complete system of representatives
, with a complete system of representatives 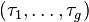 .
The order of the decomposition group
.
The order of the decomposition group 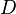 is the inertia degree
is the inertia degree 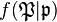 of
of 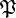 over
over  .
.
Consequently, the ideal embedding is given by 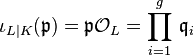 ,
and the class extension by
,
and the class extension by 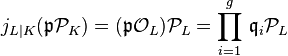 .
.
Artin's reciprocity law
Let 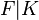 be a Galois extension of algebraic number fields with automorphism group
be a Galois extension of algebraic number fields with automorphism group 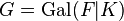 .
Suppose that
.
Suppose that 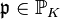 is a prime ideal of
is a prime ideal of  which does not divide the relative discriminant
which does not divide the relative discriminant 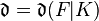 , and is therefore unramified in
, and is therefore unramified in 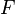 , and let
, and let 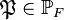 be a prime ideal of
be a prime ideal of 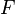 lying over
lying over 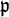 .
.
Then, there exists a unique automorphism 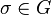 such that
such that 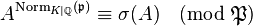 , for all algebraic integers
, for all algebraic integers 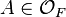 , which is called the Frobenius automorphism
, which is called the Frobenius automorphism 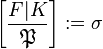 of
of 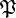 and generates the cyclic decomposition group
and generates the cyclic decomposition group 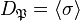 of
of 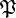 . Any other prime ideal of
. Any other prime ideal of 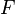 dividing
dividing 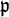 is of the form
is of the form 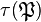 with some
with some 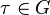 . Its Frobenius automorphism is given by
. Its Frobenius automorphism is given by 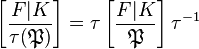 , since
, since 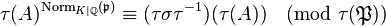 , for all
, for all 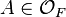 , and thus its decomposition group
, and thus its decomposition group 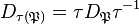 is conjugate to
is conjugate to 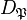 . In this general situation, the Artin symbol is a mapping
. In this general situation, the Artin symbol is a mapping 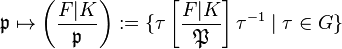 which associates an entire conjugacy class of automorphisms to any unramified prime ideal
which associates an entire conjugacy class of automorphisms to any unramified prime ideal 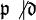 , and we have
, and we have 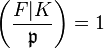 if and only if
if and only if 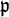 splits completely in
splits completely in 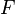 .
.
Now let 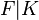 be an abelian extension, that is, the Galois group
be an abelian extension, that is, the Galois group 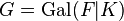 is an abelian group. Then, all conjugate decomposition groups of prime ideals of
is an abelian group. Then, all conjugate decomposition groups of prime ideals of 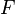 lying over
lying over 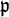 coincide
coincide 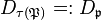 , for any
, for any 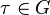 , and the Artin symbol
, and the Artin symbol 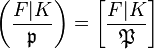 becomes equal to the Frobenius automorphism of any
becomes equal to the Frobenius automorphism of any 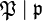 , since
, since 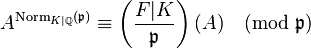 , for all
, for all 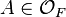 .
.
By class field theory,
[3]
the abelian extension 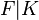 uniquely corresponds to an intermediate group
uniquely corresponds to an intermediate group 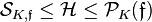 between the ray modulo
between the ray modulo 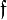 of
of  , that is
, that is  , and the group of principal ideals coprime to
, and the group of principal ideals coprime to 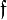 of
of  , where
, where 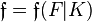 denotes the relative conductor. (Note that
denotes the relative conductor. (Note that 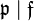 if and only if
if and only if 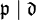 , but
, but 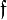 is minimal with this property.) The Artin symbol
is minimal with this property.) The Artin symbol 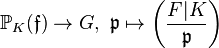 , which associates the Frobenius automorphism of
, which associates the Frobenius automorphism of 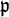 to each prime ideal
to each prime ideal 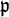 of
of  which is unramified in
which is unramified in 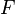 , can be extended by multiplicativity to an epimorphism
, can be extended by multiplicativity to an epimorphism 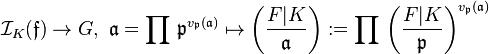 with kernel
with kernel 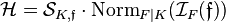 , which induces the Artin isomorphism, or Artin map,
, which induces the Artin isomorphism, or Artin map, 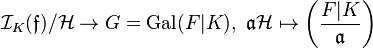 of the generalized ideal class group
of the generalized ideal class group 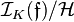 to the Galois group
to the Galois group  , which maps the class
, which maps the class 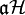 of
of 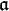 to the Artin symbol
to the Artin symbol 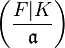 of
of 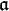 . This explicit isomorphism is called the Artin reciprocity law or general reciprocity law.
[4]
. This explicit isomorphism is called the Artin reciprocity law or general reciprocity law.
[4]

Commutative diagram
E. Artin's translation of the general principalization problem for a number field extension 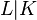 from number theory to group theory is based on the following scenario.
Let
from number theory to group theory is based on the following scenario.
Let 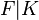 be a Galois extension of algebraic number fields with automorphism group
be a Galois extension of algebraic number fields with automorphism group 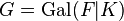 .
Suppose that
.
Suppose that 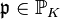 is a prime ideal of
is a prime ideal of  which does not divide the relative discriminant
which does not divide the relative discriminant 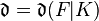 , and is therefore unramified in
, and is therefore unramified in 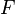 , and let
, and let 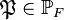 be a prime ideal of
be a prime ideal of 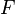 lying over
lying over 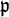 .
Assume that
.
Assume that 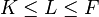 is an intermediate field with relative group
is an intermediate field with relative group 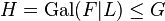 and let
and let 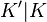 , resp.
, resp. 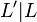 , be the maximal abelian subextension of
, be the maximal abelian subextension of  , resp.
, resp. 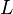 , within
, within 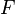 . Then, the corresponding relative groups are the commutator subgroups
. Then, the corresponding relative groups are the commutator subgroups 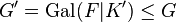 , resp.
, resp. 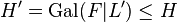 .
.
By class field theory, there exist intermediate groups 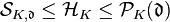 and
and 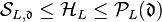 such that the Artin maps establish isomorphisms
such that the Artin maps establish isomorphisms
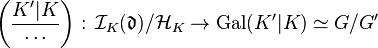 and
and
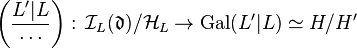 .
.
The class extension homomorphism 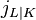 and the Artin transfer, more precisely, the induced transfer
and the Artin transfer, more precisely, the induced transfer 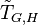 , are connected by the commutative diagram in Figure 1 via these Artin isomorphisms, that is, we have equality of two composita
, are connected by the commutative diagram in Figure 1 via these Artin isomorphisms, that is, we have equality of two composita
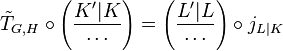 .
[5]
The justification for this statement consists in analyzing the two paths of composite mappings.
[3]
On the one hand, the class extension homomorphism
.
[5]
The justification for this statement consists in analyzing the two paths of composite mappings.
[3]
On the one hand, the class extension homomorphism 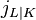 maps the generalized ideal class
maps the generalized ideal class 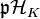 of the base field
of the base field  to the extension class
to the extension class 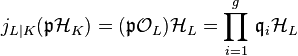 in the field
in the field 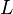 , and the Artin isomorphism
, and the Artin isomorphism 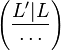 of the field
of the field 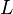 maps this product of classes of prime ideals to the product of conjugates of Frobenius automorphisms
maps this product of classes of prime ideals to the product of conjugates of Frobenius automorphisms
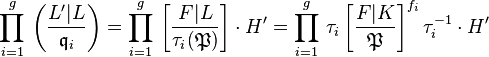 . Here, the double coset decomposition and its representatives were used, in perfect analogy to the last but one section.
On the other hand, the Artin isomorphism
. Here, the double coset decomposition and its representatives were used, in perfect analogy to the last but one section.
On the other hand, the Artin isomorphism 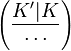 of the base field
of the base field  maps the generalized ideal class
maps the generalized ideal class 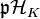 to the Frobenius automorphism
to the Frobenius automorphism 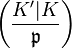 , and
the induced Artin transfer maps the symbol
, and
the induced Artin transfer maps the symbol 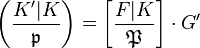 to the product
to the product
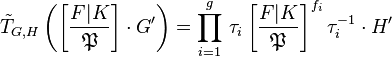 .
[6]
This product expression was the original form of the Artin transfer homomorphism, corresponding to a decomposition of the permutation representation into disjoint cycles.
.
[6]
This product expression was the original form of the Artin transfer homomorphism, corresponding to a decomposition of the permutation representation into disjoint cycles.
Class field tower
The commutative diagram in the previous section, which connects the number theoretic class extension homomorphism 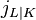 with the group theoretic Artin transfer
with the group theoretic Artin transfer 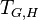 , enabled Furtwängler to prove the principal ideal theorem by specializing to the situation that
, enabled Furtwängler to prove the principal ideal theorem by specializing to the situation that 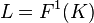 is the first Hilbert class field of
is the first Hilbert class field of  , that is the maximal abelian unramified extension of
, that is the maximal abelian unramified extension of  , and
, and 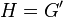 is the commutator subgroup of
is the commutator subgroup of  . More precisely, Furtwängler showed that generally the Artin transfer
. More precisely, Furtwängler showed that generally the Artin transfer 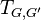 from a metabelian group
from a metabelian group  to its derived subgroup
to its derived subgroup 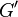 maps all elements of
maps all elements of  to the neutral element of
to the neutral element of 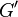 .
.
However, the commutative diagram comprises the potential for a lot of more sophisticated applications. In the situation that 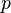 is a prime number,
is a prime number,
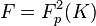 is the second Hilbert p-class field of
is the second Hilbert p-class field of  , that is the maximal metabelian unramified extension of
, that is the maximal metabelian unramified extension of  of degree a power of
of degree a power of 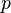 ,
,
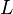 varies over the intermediate field between
varies over the intermediate field between  and its first Hilbert p-class field
and its first Hilbert p-class field 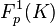 ,
and
,
and 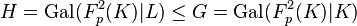 correspondingly varies over the intermediate groups between
correspondingly varies over the intermediate groups between  and
and 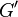 ,
computation of all principalization kernels
,
computation of all principalization kernels 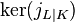 and all p-class groups
and all p-class groups 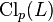 translates to information on the kernels
translates to information on the kernels 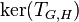 and targets
and targets 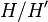 of the Artin transfers
of the Artin transfers 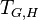 and permits the exact specification of the second p-class group
and permits the exact specification of the second p-class group 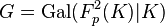 of
of  via pattern recognition, and frequently even allows to draw conclusions about the entire p-class field tower of
via pattern recognition, and frequently even allows to draw conclusions about the entire p-class field tower of  ,
that is the Galois group
,
that is the Galois group  of the maximal unramified pro-p extension
of the maximal unramified pro-p extension 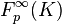 of
of  .
.
These ideas are explicit in the paper of 1934 by A. Scholz and O. Taussky already. [7] At these early stages, pattern recognition consisted of specifying the annihilator ideals, or symbolic orders, and the Schreier relations of metabelian p-groups and subsequently using a uniqueness theorem on group extensions by O. Schreier. [8] Nowadays, we use the p-group generation algorithm of M. F. Newman [9] and E. A. O'Brien [10] for constructing descendant trees of p-groups and searching patterns, defined by kernels and targets of Artin transfers, among the vertices of these trees.
Galois cohomology
In the chapter on cyclic relative extensions of prime degree of his number report 1897, D. Hilbert
[2]
proves a series of crucial theorems which culminate in Theorem 94, the original germ of class field theory. Today, these theorems can be viewed as the beginning of what is now called Galois cohomology. Hilbert considers a finite relative extension 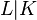 of algebraic number fields with cyclic Galois group
of algebraic number fields with cyclic Galois group 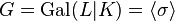 generated by an automorphism
generated by an automorphism 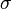 such that
such that 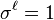 for the relative degree
for the relative degree 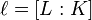 , which is assumed to be an odd prime.
, which is assumed to be an odd prime.
He investigates two endomorphism of the unit group 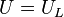 of the extension field, viewed as a Galois module with respect to the group
of the extension field, viewed as a Galois module with respect to the group  , briefly a
, briefly a  -module. The first endomorphism
-module. The first endomorphism 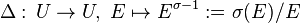 is the symbolic exponentiation with the difference
is the symbolic exponentiation with the difference 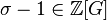 , and the second endomorphism
, and the second endomorphism 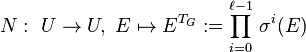 is the algebraic norm mapping, that is the symbolic exponentiation with the trace
is the algebraic norm mapping, that is the symbolic exponentiation with the trace 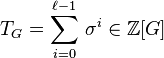 . In fact, the image of the algebraic norm map is contained in the unit group
. In fact, the image of the algebraic norm map is contained in the unit group 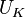 of the base field, and thus
of the base field, and thus 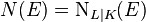 coincides with the usual arithmetic norm as the product of all conjugates. The composita of the endomorphisms satisfy the relations
coincides with the usual arithmetic norm as the product of all conjugates. The composita of the endomorphisms satisfy the relations 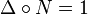 and
and 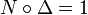 .
.
Two important cohomology groups can be defined by means of the kernels and images of these endomorphisms. The zeroth cohomology group of  in
in 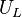 is given by the quotient
is given by the quotient 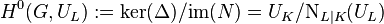 consisting of the norm residues of
consisting of the norm residues of 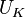 , and the minus first cohomology group of
, and the minus first cohomology group of  in
in 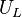 is given by the quotient
is given by the quotient 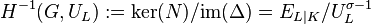 of the group
of the group 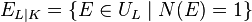 of relative units of
of relative units of 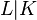 modulo the subgroup of symbolic powers of units with formal exponent
modulo the subgroup of symbolic powers of units with formal exponent 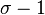 .
.
In his Theorem 92, under the additional assumption that 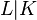 be unramified,
Hilbert proves the existence of a relative unit
be unramified,
Hilbert proves the existence of a relative unit 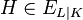 which cannot be expressed as
which cannot be expressed as 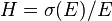 , for any unit
, for any unit 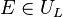 , which means that the minus first cohomology group
, which means that the minus first cohomology group 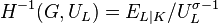 is non-trivial of order divisible by
is non-trivial of order divisible by 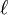 . However, with the aid of a completely similar construction, the minus first cohomology group
. However, with the aid of a completely similar construction, the minus first cohomology group 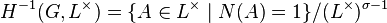 of the
of the  -module
-module 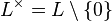 , the multiplicative group of the superfield
, the multiplicative group of the superfield 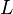 , can be defined, and Hilbert shows its triviality
, can be defined, and Hilbert shows its triviality 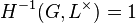 in Theorem 90. Applied to the particular unit
in Theorem 90. Applied to the particular unit 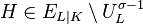 , this ensures the existence of a non-unit
, this ensures the existence of a non-unit 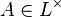 such that
such that 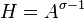 , i. e.,
, i. e., 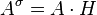 .
.
The non-unit  is generator of an ambiguous principal ideal of
is generator of an ambiguous principal ideal of 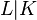 , since
, since 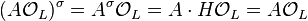 .
However, the underlying ideal
.
However, the underlying ideal 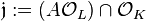 of the subfield
of the subfield  cannot be principal, because otherwise we had
cannot be principal, because otherwise we had 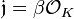 , consequently
, consequently 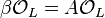 , and thus
, and thus 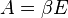 for some unit
for some unit 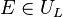 .
This would imply the contradiction
.
This would imply the contradiction 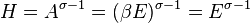 , since
, since 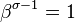 .
The ideal
.
The ideal 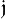 has yet another interesting property. The
has yet another interesting property. The 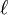 th power of its extension ideal
th power of its extension ideal 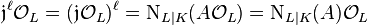 coincides with its relative norm and thus, by forming the intersection with
coincides with its relative norm and thus, by forming the intersection with 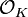 , turns out to be principal in the base field
, turns out to be principal in the base field  already.
already.
Eventually, Hilbert is in the position to state his celebrated Theorem 94: If 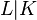 is a cyclic extension of number fields of odd prime degree
is a cyclic extension of number fields of odd prime degree 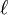 with trivial relative discriminant
with trivial relative discriminant 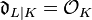 , that is, an unramified extension, then there exists a non-principal ideal
, that is, an unramified extension, then there exists a non-principal ideal 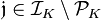 of the base field
of the base field  which becomes principal
which becomes principal 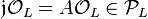 in the extension field
in the extension field 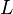 , but the
, but the 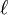 th power of this non-principal ideal is principal
th power of this non-principal ideal is principal 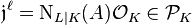 in the base field
in the base field  already. Hence, the class number of the base field must be divisible by
already. Hence, the class number of the base field must be divisible by 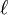 and the extension field
and the extension field 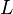 can be called a class field of
can be called a class field of  .
.
Theorem 94 includes the simple inequality 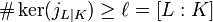 for the order of the principalization kernel of the extension
for the order of the principalization kernel of the extension 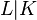 .
However, an improved estimate by a possibly bigger lower bound can be derived by means of the theorem on the Herbrand quotient
[11]
.
However, an improved estimate by a possibly bigger lower bound can be derived by means of the theorem on the Herbrand quotient
[11]
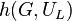 of the
of the  -module
-module 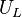 , which is given by
, which is given by
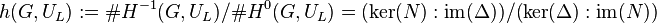
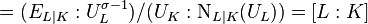 ,
where
,
where 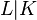 is a (not necessarily unramified) relative extension of odd degree
is a (not necessarily unramified) relative extension of odd degree 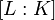 (not necessarily a prime) with cyclic Galois group
(not necessarily a prime) with cyclic Galois group 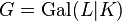 .
With the aid of K. Iwasawa's isomorphism
[12]
between the first cohomology group
.
With the aid of K. Iwasawa's isomorphism
[12]
between the first cohomology group 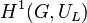 of
of  in
in 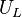 and the quotient
and the quotient 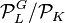 of the group of ambiguous principal ideals of
of the group of ambiguous principal ideals of 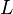 modulo the group of principal ideals of
modulo the group of principal ideals of  , for any Galois extension
, for any Galois extension 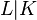 with automorphism group
with automorphism group 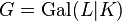 , specialized to a cyclic extension with periodic cohomology of length
, specialized to a cyclic extension with periodic cohomology of length 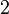 , and observing that
, and observing that 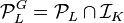 consists of extension ideals only when
consists of extension ideals only when 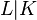 is unramified, we obtain
is unramified, we obtain
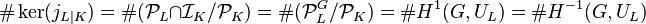
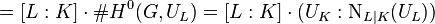 .
This relation increases the lower bound by the factor
.
This relation increases the lower bound by the factor 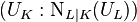 , the so-called unit norm index.
, the so-called unit norm index.
History
As mentioned in the lead section, several investigators tried to generalize the Hilbert-Artin-Furtwängler principal ideal theorem of 1930 to questions concerning the principalization in intermediate extensions between the base field and its Hilbert cass field. On the one hand, they established general theorems on the principalization over arbitrary number fields, such as Ph. Furtwängler 1932, [13] O. Taussky 1932, [14] O. Taussky 1970, [15] and H. Kisilevsky 1970. [16] On the other hand, they searched for concrete numerical examples of principalization in unramified cyclic extensions of particular kinds of base fields.
Quadratic fields
The principalization of 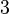 -classes of complex quadratic number fields
-classes of complex quadratic number fields 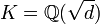 with
with 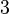 -class rank two in unramified cyclic cubic extensions was calculated manually for three discriminants
-class rank two in unramified cyclic cubic extensions was calculated manually for three discriminants 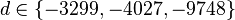 by A. Scholz and O. Taussky
[7]
in 1934. Since these calculations require composition of binary quadratic forms and explicit knowledge of fundamental systems of units in cubic number fields, which was a very difficult task in 1934, the investigations stayed at rest for half a century until F.-P. Heider and B. Schmithals
[17]
employed the CDC Cyber 76 computer at the University of Cologne to extend the information concerning principalization to the range
by A. Scholz and O. Taussky
[7]
in 1934. Since these calculations require composition of binary quadratic forms and explicit knowledge of fundamental systems of units in cubic number fields, which was a very difficult task in 1934, the investigations stayed at rest for half a century until F.-P. Heider and B. Schmithals
[17]
employed the CDC Cyber 76 computer at the University of Cologne to extend the information concerning principalization to the range 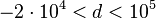 containing
containing 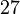 relevant discriminants in 1982,
thereby providing the first analysis of five real quadratic fields.
Two years later, J. R. Brink
[18]
computed the principalization types of
relevant discriminants in 1982,
thereby providing the first analysis of five real quadratic fields.
Two years later, J. R. Brink
[18]
computed the principalization types of 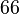 complex quadratic fields.
Currently, the most extensive computation of principalization data for all
complex quadratic fields.
Currently, the most extensive computation of principalization data for all 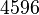 quadratic fields with discriminants
quadratic fields with discriminants 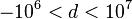 and
and 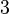 -class group of type
-class group of type 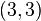 is due to D. C. Mayer in 2010,
[19]
who used his recently discovered connection between transfer kernels and transfer targets for the design of a new principalization algorithm.
[20]
is due to D. C. Mayer in 2010,
[19]
who used his recently discovered connection between transfer kernels and transfer targets for the design of a new principalization algorithm.
[20]
The 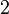 -principalization in unramified quadratic extensions of complex quadratic fields with
-principalization in unramified quadratic extensions of complex quadratic fields with 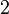 -class group of type
-class group of type 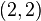 was studied by H. Kisilevsky in 1976.
[21]
Similar investigations of real quadratic fields were carried out by E. Benjamin and C. Snyder in 1995.
[22]
was studied by H. Kisilevsky in 1976.
[21]
Similar investigations of real quadratic fields were carried out by E. Benjamin and C. Snyder in 1995.
[22]
Cubic fields
The 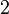 -principalization in unramified quadratic extensions of cyclic cubic number fields with
-principalization in unramified quadratic extensions of cyclic cubic number fields with 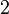 -class group of type
-class group of type 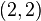 was investigated by A. Derhem in 1988.
[23]
Seven years later, M. Ayadi studied the
was investigated by A. Derhem in 1988.
[23]
Seven years later, M. Ayadi studied the 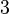 -principalization in unramified cyclic cubic extensions of cyclic cubic fields
-principalization in unramified cyclic cubic extensions of cyclic cubic fields 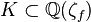 ,
, 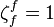 , with
, with 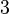 -class group of type
-class group of type 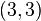 and conductor
and conductor  divisible by two or three primes.
[24]
divisible by two or three primes.
[24]
Sextic fields
In 1992, M. C. Ismaili investigated the 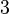 -principalization in unramified cyclic cubic extensions of the normal closure of pure cubic fields
-principalization in unramified cyclic cubic extensions of the normal closure of pure cubic fields ![K=\mathbb{Q}(\sqrt[3]{D})](../I/m/ec5dbb407b05ccee76de27c38bd88bc0.png) , in the case that this sextic number field
, in the case that this sextic number field 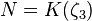 ,
, 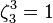 , has a
, has a 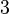 -class group of type
-class group of type 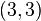 .
[25]
.
[25]
Quartic fields
In 1993, A. Azizi studied the 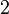 -principalization in unramified quadratic extensions of bicyclic biquadratic fields of Dirichlet type
-principalization in unramified quadratic extensions of bicyclic biquadratic fields of Dirichlet type 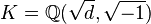 with
with 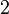 -class group of type
-class group of type 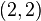 .
[26]
Most recently, in 2014, A. Zekhnini extended the investigations to Dirichlet fields with
.
[26]
Most recently, in 2014, A. Zekhnini extended the investigations to Dirichlet fields with 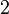 -class group of type
-class group of type 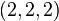 ,
[27]
thus providing the first examples of
,
[27]
thus providing the first examples of 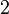 -principalization in the two layers of unramified quadratic and biquadratic extensions of quartic fields with class groups of
-principalization in the two layers of unramified quadratic and biquadratic extensions of quartic fields with class groups of 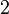 -rank three.
-rank three.
See also
Both, the algebraic, group theoretic access to the principalization problem by Hilbert-Artin-Furtwängler and the arithmetic, cohomological access by Hilbert-Herbrand-Iwasawa are also presented in detail in the two bibles of capitulation by J.-F. Jaulent 1988 [28] and by K. Miyake 1989. [5]
Secondary sources
- Cassels, J.W.S.; Fröhlich, Albrecht, eds. (1967). Algebraic Number Theory. Academic Press. Zbl 0153.07403.
- Iwasawa, Kenkichi (1986). Local class field theory. Oxford Mathematical Monographs. Oxford University Press. ISBN 978-0-19-504030-2. MR 863740. Zbl 0604.12014.
- Janusz, Gerald J. (1973). Algebraic number fields. Pure and Applied Mathematics 55. Academic Press. p. 142. Zbl 0307.12001.
- Neukirch, Jürgen (1999). Algebraic Number Theory. Grundlehren der Mathematischen Wissenschaften 322. Springer-Verlag. ISBN 978-3-540-65399-8. MR 1697859. Zbl 0956.11021.
- Neukirch, Jürgen; Schmidt, Alexander; Wingberg, Kay (2008). Cohomology of Number Fields. Grundlehren der Mathematischen Wissenschaften 323 (2nd ed.). Springer-Verlag. ISBN 3-540-37888-X. Zbl 1136.11001.
References
- ↑ Hurwitz, A. (1926). "Über Beziehungen zwischen den Primidealen eines algebraischen Körpers und den Substitutionen seiner Gruppe". Math. Z. 25: 661–665. doi:10.1007/bf01283860.
- ↑ 2.0 2.1 Hilbert, D. (1897). "Die Theorie der algebraischen Zahlkörper". Jahresber. Deutsch. Math. Verein. 4: 175–546.
- ↑ 3.0 3.1 Hasse, H. (1930). "Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraischen Zahlkörper. Teil II: Reziprozitätsgesetz". Jahresber. Deutsch. Math. Verein., Ergänzungsband 6: 1–204.
- ↑ Artin, E. (1927). "Beweis des allgemeinen Reziprozitätsgesetzes". Abh. Math. Sem. Univ. Hamburg 5: 353–363.
- ↑ 5.0 5.1 Miyake, K. (1989). "Algebraic investigations of Hilbert's Theorem 94, the principal ideal theorem and the capitulation problem". Expo. Math. 7: 289–346.
- ↑ Artin, E. (1929). "Idealklassen in Oberkörpern und allgemeines Reziprozitätsgesetz". Abh. Math. Sem. Univ. Hamburg 7: 46–51.
- ↑ 7.0 7.1 Scholz, A., Taussky, O. (1934). "Die Hauptideale der kubischen Klassenkörper imaginär quadratischer Zahlkörper: ihre rechnerische Bestimmung und ihr Einfluß auf den Klassenkörperturm". J. Reine Angew. Math. 171: 19–41.
- ↑ Schreier, O. (1926). "Über die Erweiterung von Gruppen II". Abh. Math. Sem. Univ. Hamburg 4: 321–346.
- ↑ Newman, M. F. (1977). Determination of groups of prime-power order. pp. 73-84, in: Group Theory, Canberra, 1975, Lecture Notes in Math., Vol. 573, Springer, Berlin.
- ↑ O'Brien, E. A. (1990). "The p-group generation algorithm". J. Symbolic Comput. 9: 677–698. doi:10.1016/s0747-7171(08)80082-x.
- ↑ Herbrand, J. (1932). "Sur les théorèmes du genre principal et des idéaux principaux". Abh. Math. Sem. Univ. Hamburg 9: 84–92. doi:10.1007/bf02940630.
- ↑ Iwasawa, K. (1956). "A note on the group of units of an algebraic number field". J. Math. Pures Appl. 9 (35): 189–192.
- ↑ Furtwängler, Ph. (1932). "Über eine Verschärfung des Hauptidealsatzes für algebraische Zahlkörper". J. Reine Angew. Math. 167: 379–387.
- ↑ Taussky, O. (1932). "Über eine Verschärfung des Hauptidealsatzes für algebraische Zahlkörper". J. Reine Angew. Math. 168: 193–210.
- ↑ Taussky, O. (1970). "A remark concerning Hilbert's Theorem 94". J. Reine Angew. Math. 239/240: 435–438.
- ↑ Kisilevsky, H. (1970). "Some results related to Hilbert's Theorem 94". J. Number Theory 2: 199–206. doi:10.1016/0022-314x(70)90020-x.
- ↑ Heider, F.-P., Schmithals, B. (1982). "Zur Kapitulation der Idealklassen in unverzweigten primzyklischen Erweiterungen". J. Reine Angew. Math. 363: 1–25.
- ↑ Brink, J. R. (1984). The class field tower for imaginary quadratic number fields of type (3,3). Dissertation, Ohio State Univ.
- ↑ Mayer, D. C. (2012). "The second p-class group of a number field". Int. J. Number Theory 8 (2): 471–505. doi:10.1142/s179304211250025x.
- ↑ Mayer, D. C. (2014). "Principalization algorithm via class group structure". J. Théor. Nombres Bordeaux 26 (2): 415–464.
- ↑ Kisilevsky, H. (1976). "Number fields with class number congruent to 4 mod 8 and Hilbert's Theorem 94". J. Number Theory 8: 271–279. doi:10.1016/0022-314x(76)90004-4.
- ↑ Benjamin, E., Snyder, C. (1995). "Real quadratic number fields with 2-class group of type (2,2)". Math. Scand. 76: 161–178.
- ↑ Derhem, A. (1988). Capitulation dans les extensions quadratiques non ramifiées de corps de nombres cubiques cycliques. Thèse de Doctorat, Univ. Laval, Québec.
- ↑ Ayadi, M. (1995). Sur la capitulation de 3-classes d'idéaux d'un corps cubique cyclique. Thèse de Doctorat, Univ. Laval, Québec.
- ↑ Ismaili, M. C. (1992). Sur la capitulation de 3-classes d'idéaux de la clôture normale d'un corps cubique pure. Thèse de Doctorat, Univ. Laval, Québec.
- ↑ Azizi, A. (1993). Sur la capitulation de 2-classes d'idéaux de
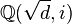 . Thèse de Doctorat, Univ. Laval, Québec.
. Thèse de Doctorat, Univ. Laval, Québec.
- ↑ Zekhnini, A. (2014). Capitulation des 2-classes d'idéaux de certains corps de nombres biquadratiques imaginaires
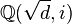 de type (2,2,2). Thèse de Doctorat, Univ. Mohammed Premier, Faculté des Sciences d'Oujda, Maroc.
de type (2,2,2). Thèse de Doctorat, Univ. Mohammed Premier, Faculté des Sciences d'Oujda, Maroc.
- ↑ Jaulent, J.-F. (26 February 1988). "L'état actuel du problème de la capitulation". Séminaire de Théorie des Nombres de Bordeaux 17: 1–33.