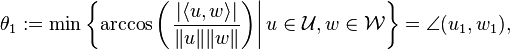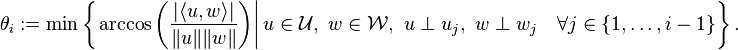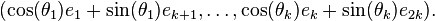Principal angles
In linear algebra (mathematics), the principal angles, also called canonical angles, provide information about the relative position of two subspaces of an inner product space. The concept was first introduced by Jordan in 1875.
Definition
Let  be an inner product space.
Given two subspaces
be an inner product space.
Given two subspaces 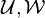 with
with
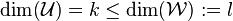 ,
there exists then a sequence of
,
there exists then a sequence of  angles
angles
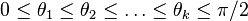 called the principal angles, the first one defined as
called the principal angles, the first one defined as
where 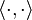 is the inner product and
is the inner product and  the induced norm. The vectors
the induced norm. The vectors 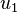 and
and 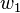 are the corresponding principal vectors.
are the corresponding principal vectors.
The other principal angles and vectors are then defined recursively via
This means that the principal angles
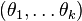 form a set of minimized angles between the two subspaces, and the principal vectors in each subspace are orthogonal to each other.
form a set of minimized angles between the two subspaces, and the principal vectors in each subspace are orthogonal to each other.
Examples
Geometric Example
Geometrically, subspaces are flats (points, lines, planes etc.) that include the origin, thus any two subspaces intersect at least in the origin. Two two-dimensional subspaces 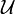 and
and 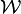 generate a set of two angles. In a three-dimensional Euclidean space, the subspaces
generate a set of two angles. In a three-dimensional Euclidean space, the subspaces 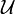 and
and 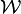 are either identical, or their intersection forms a line. In the former case, both
are either identical, or their intersection forms a line. In the former case, both 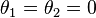 . In the latter case, only
. In the latter case, only 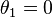 , where vectors
, where vectors 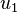 and
and 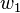 are on the line of the intersection
are on the line of the intersection 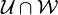 and have the same direction. The angle
and have the same direction. The angle 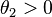 will be the angle between the subspaces
will be the angle between the subspaces 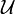 and
and 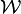 in the orthogonal complement to
in the orthogonal complement to 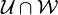 . Imagining the angle between two planes in 3D, one intuitively thinks of the largest angle,
. Imagining the angle between two planes in 3D, one intuitively thinks of the largest angle, 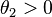 .
.
Algebraic Example
In 4-dimensional real coordinate space R4, let the two-dimensional subspace 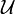 be
spanned by
be
spanned by 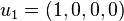 and
and 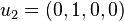 , while the two-dimensional subspace
, while the two-dimensional subspace 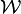 be
spanned by
be
spanned by 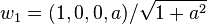 and
and 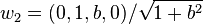 with some real
with some real  and
and  such that
such that 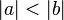 . Then
. Then 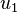 and
and 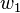 are, in fact, the pair of principal vectors corresponding to the angle
are, in fact, the pair of principal vectors corresponding to the angle 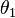 with
with 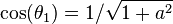 , and
, and 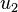 and
and 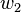 are the principal vectors corresponding to the angle
are the principal vectors corresponding to the angle 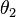 with
with 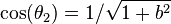
To construct a pair of subspaces with any given set of  angles
angles 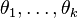 in a
in a 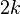 (or larger) dimensional Euclidean space, take a subspace
(or larger) dimensional Euclidean space, take a subspace 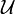 with an orthonormal basis
with an orthonormal basis 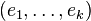 and complete it to an orthonormal basis
and complete it to an orthonormal basis 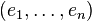 of the Euclidean space, where
of the Euclidean space, where 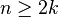 . Then, an orthonormal basis of the other subspace
. Then, an orthonormal basis of the other subspace 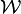 is, e.g.,
is, e.g.,
Basic Properties
If the largest angle is zero, one subspace is a subset of the other.
If the smallest angle is zero, the subspaces intersect at least in a line.
The number of angles equal to zero is the dimension of the space where the two subspaces intersect.
References
- Concerning the angles and the angular determination English lecture dealing with the original work of Jordan read by Keyeser, 1902.
- Principal angles in terms of inner product Downloadable note on the construction of principal angles, Shonkwiler, Haverford