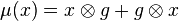Primitive element (co-algebra)
In algebra, a primitive element of a co-algebra C (over an element g) is an element x that satisfies
where 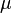 is the co-multiplication and g is an element of C that maps to the multiplicative identity 1 of the base field under the co-unit (g is called group-like). C is said to be primitively generated if it is generated by primitive elements.
is the co-multiplication and g is an element of C that maps to the multiplicative identity 1 of the base field under the co-unit (g is called group-like). C is said to be primitively generated if it is generated by primitive elements.
If C is a bi-algebra; i.e., a co-algebra that is also an algebra, then one usually takes g to be 1, the multiplicative identity of C.
If C is a bi-algebra, then the set of primitive elements form a Lie algebra with the usual commutator bracket ![[x, y] = xy - yx](../I/m/2d4099ee292ebfa424a594a8233f6a38.png) (graded commutator if C is graded.)
(graded commutator if C is graded.)
If A is a (certain graded) Hopf algebra over a field of characteristic zero, then the Milnor–Moore theorem states the universal enveloping algebra of the graded Lie algebra of primitive elements of A is isomorphic to A.