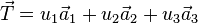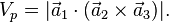Primitive cell

The parallelogram is the general primitive cell for the plane.

A parallelepiped is a general primitive cell for 3-dimensional space.

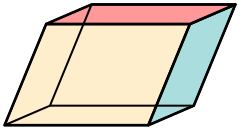
A primitive cell is a unit cell constructed so that it contains only one lattice point (each vertice of the cell sits on a lattice point which is shared with the surrounding cells, each lattice point is said to contribute 1/n to the total number of lattice points in the cell where n is the number of cells sharing the lattice point).^[1] A primitive cell is built on the primitive basis of the direct lattice, namely a crystallographic basis of the vector lattice L such that every lattice vector t of L may be obtained as an integral linear combination of the basis vectors, a, b, c.

Used predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum volume cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions. A lattice can be characterized by the geometry of its primitive cell.

The primitive cell is a fundamental domain with respect to translational symmetry only. In the case of additional symmetries a fundamental domain is smaller.

A crystal can be categorized by its lattice and the atoms that lie in a primitive cell (the basis). A cell will fill all the lattice space without leaving gaps by repetition of crystal translation operations.

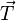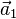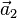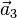Primitive translation vectors are used to define a crystal translation vector, $\vec T$ , and also gives a lattice cell of smallest volume for a particular lattice. The lattice and translation vectors $\vec a_1$ , $\vec a_2$ , and $\vec a_3$ are primitive if the atoms look the same from any lattice points using integers 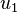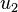$u_1$ , $u_2$ , and $u_3$ .

\vec T = u_1\vec a_1 + u_2\vec a_2 + u_3\vec a_3

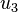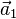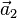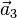The primitive cell is defined by the primitive axes (vectors) $\vec a_1$ , $\vec a_2$ , and $\vec a_3$ . The volume, $V_p$ , of the primitive cell is given by the parallelepiped from the above axes as

V_p = | \vec a_1 \cdot ( \vec a_2 \times \vec a_3 ) |.

References

↑ "DoITPoMS - TLP Library Crystallography - Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.

Primitive cell

See also

References