Prime avoidance lemma

In algebra, the prime avoidance lemma says that if an ideal I in a commutative ring R is contained in a union of finitely many prime ideals P_i's, then it is contained in P_i for some i.

There are many variations of the lemma (cf. Hochster); for example, if the ring R contains an infinite field (or a finite field of sufficiently large cardinarity), then the statement follows from a fact in linear algebra that a vector space over an infinite field is not a finite union of its proper vector subspaces. (Proof of the fact: suppose the vector space is a finite union of proper subspaces. Consider a finite product of linear functionals, each of which vanishes on a proper subspace that appears in the union; then it is a nonzero polynomial vanishing identically, a contradiction.)

Statement and proof

The following statement and argument are perhaps the most standard.

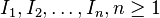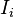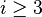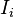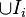Statement: Let E be a subset of R that is an additive subgroup of R and is multiplicatively closed. Let $I_1, I_2, \dots, I_n, n \ge 1$ be ideals such that $I_i$ are prime ideals for $i \ge 3$ . If E is not contained in any of $I_i$ 's, then E is not contained in the union $\cup I_i$ .

Proof by induction on n: The idea is to find an element that is in E and not in any of 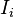$I_i$ 's. The basic case n = 1 is trivial. Next suppose n ≥ 2. For each i choose

z_i \in E - \cup_{j \ne i} I_j

where the set on the right is nonempty by inductive hypothesis. We can assume 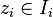$z_i \in I_i$ for all i; otherwise, some 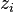$z_i$ avoids all the 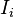$I_i$ 's and we are done. Put

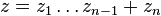z = z_1 \dots z_{n-1} + z_n

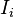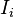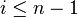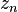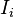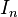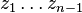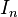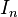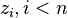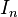Then z is in E but not in any of $I_i$ 's. Indeed, if z is in $I_i$ for some $i \le n - 1$ , then $z_n$ is in $I_i$ , a contradiction. Suppose z is in $I_n$ . Then $z_1 \dots z_{n-1}$ is in $I_n$ . If n is 2, we are done. If n > 2, then, since $I_n$ is a prime ideal, some $z_i, i < n$ is in $I_n$ , a contradiction.

References

Mel Hochster, Dimension theory and systems of parameters, a supplementary note