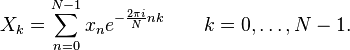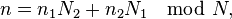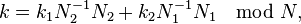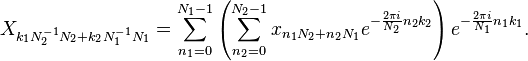Prime-factor FFT algorithm

The prime-factor algorithm (PFA), also called the Good–Thomas algorithm (1958/1963), is a fast Fourier transform (FFT) algorithm that re-expresses the discrete Fourier transform (DFT) of a size N = N1N2 as a two-dimensional N1×N2 DFT, but only for the case where N1 and N2 are relatively prime. These smaller transforms of size N1 and N2 can then be evaluated by applying PFA recursively or by using some other FFT algorithm.

PFA should not be confused with the mixed-radix generalization of the popular Cooley–Tukey algorithm, which also subdivides a DFT of size N = N1N2 into smaller transforms of size N1 and N2. The latter algorithm can use any factors (not necessarily relatively prime), but it has the disadvantage that it also requires extra multiplications by roots of unity called twiddle factors, in addition to the smaller transforms. On the other hand, PFA has the disadvantages that it only works for relatively prime factors (e.g. it is useless for power-of-two sizes) and that it requires a more complicated re-indexing of the data based on the Chinese remainder theorem (CRT). Note, however, that PFA can be combined with mixed-radix Cooley–Tukey, with the former factorizing N into relatively prime components and the latter handling repeated factors.

PFA is also closely related to the nested Winograd FFT algorithm, where the latter performs the decomposed N1 by N2 transform via more sophisticated two-dimensional convolution techniques. Some older papers therefore also call Winograd's algorithm a PFA FFT.

(Although the PFA is distinct from the Cooley–Tukey algorithm, Good's 1958 work on the PFA was cited as inspiration by Cooley and Tukey in their famous 1965 paper, and there was initially some confusion about whether the two algorithms were different. In fact, it was the only prior FFT work cited by them, as they were not then aware of the earlier research by Gauss and others.)

Algorithm

Recall that the DFT is defined by the formula:

X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} nk } \qquad k = 0,\dots,N-1.

The PFA involves a re-indexing of the input and output arrays, which when substituted into the DFT formula transforms it into two nested DFTs (a two-dimensional DFT).

Re-indexing

Suppose that N = N1N2, where N1 and N2 are relatively prime. In this case, we can define a bijective re-indexing of the input n and output k by:

n = n_1 N_2 + n_2 N_1 \mod N,
k = k_1 N_2^{-1} N_2 + k_2 N_1^{-1} N_1 \mod N,

where N1−1 denotes the modular multiplicative inverse of N1 modulo N2 and vice versa for N2−1; the indices ka and na run from 0,...,Na−1 (for a = 1, 2). These inverses only exist for relatively prime N1 and N2, and that condition is also required for the first mapping to be bijective.

This re-indexing of n is called the Ruritanian mapping (also Good's mapping), while this re-indexing of k is called the CRT mapping. The latter refers to the fact that k is the solution to the Chinese remainder problem k = k1 mod N1 and k = k2 mod N2.

(One could instead use the Ruritanian mapping for the output k and the CRT mapping for the input n, or various intermediate choices.)

A great deal of research has been devoted to schemes for evaluating this re-indexing efficiently, ideally in-place, while minimizing the number of costly modulo (remainder) operations (Chan, 1991, and references).

DFT re-expression

The above re-indexing is then substituted into the formula for the DFT, and in particular into the product nk in the exponent. Because e2πi = 1, this exponent is evaluated modulo N: any N1N2 = N cross term in the nk product can be set to zero. (Similarly, Xk and xn are implicitly periodic in N, so their subscripts are evaluated modulo N.) The remaining terms give:

X_{k_1 N_2^{-1} N_2 + k_2 N_1^{-1} N_1} = \sum_{n_1=0}^{N_1-1} \left( \sum_{n_2=0}^{N_2-1} x_{n_1 N_2 + n_2 N_1} e^{-\frac{2\pi i}{N_2} n_2 k_2 } \right) e^{-\frac{2\pi i}{N_1} n_1 k_1 }.

The inner and outer sums are simply DFTs of size N2 and N1, respectively.

(Here, we have used the fact that N1−1N1 is unity when evaluated modulo N2 in the inner sum's exponent, and vice versa for the outer sum's exponent.)

References

See also