Presheaf (category theory)
In category theory, a branch of mathematics, a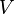 
-valued presheaf 
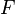on a category 
is a functor 
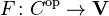. Often presheaf is defined to be a Set-valued presheaf. If is the poset of open sets in a topological space, interpreted as a category, then one recovers the usual notion of presheaf on a topological space.
A morphism of presheaves is defined to be a natural transformation of functors. This makes the collection of all presheaves into a category, and is an example of a functor category. It is often written as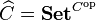 
. A functor into 
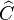is sometimes called a profunctor.
A presheaf that is naturally isomorphic to the contravariant hom-functor Hom(–,A) for some object A of C is called a representable presheaf.
Examples
- A simplicial set is a Set-valued presheaf on the simplex category
.
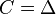Properties
- When is a small category, the functor category 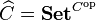is cartesian closed.
- The partially ordered set of subobjects of
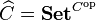form a Heyting algebra, whenever is an object of for small . - For any morphism
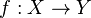of 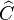, the pullback functor of subobjects 
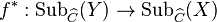has a right adjoint, denoted 
, and a left adjoint, 
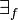. These are the universal and existential quantifiers. - A locally small category embeds fully and faithfully into the category 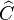of set-valued presheaves via the Yoneda embedding
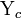which to every object 
of associates the hom-set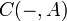 
. - The presheaf category 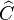is (up to equivalence of categories) the free colimit completion of the category .