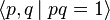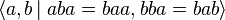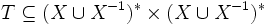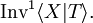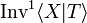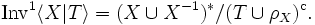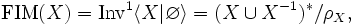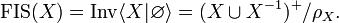Presentation of a monoid

In algebra, a presentation of a monoid (or semigroup) is a description of a monoid (or semigroup) in terms of a set Σ of generators and a set of relations on the free monoid Σ^∗ (or free semigroup Σ⁺) generated by Σ. The monoid is then presented as the quotient of the free monoid by these relations. This is an analogue of a group presentation in group theory.

As a mathematical structure, a monoid presentation is identical to a string rewriting system (also known as semi-Thue system). Every monoid may be presented by a semi-Thue system (possibly over an infinite alphabet).^[1]

A presentation should not be confused with a representation.

Construction

The relations are given as a (finite) binary relation R on Σ^∗. To form the quotient monoid, these relations are extended to monoid congruences as follows.

First, one takes the symmetric closure R ∪ R⁻¹ of R. This is then extended to a symmetric relation E ⊂ Σ^∗ × Σ^∗ by defining x ~_E y if and only if x = sut and y = svt for some strings u, v, s, t ∈ Σ^∗ with (u,v) ∈ R ∪ R⁻¹. Finally, one takes the reflexive and transitive closure of E, which is then a monoid congruence.

In the typical situation, the relation R is simply given as a set of equations, so that 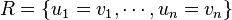$R=\{u_1=v_1,\cdots,u_n=v_n\}$ . Thus, for example,

\langle p,q\,\vert\; pq=1\rangle

is the equational presentation for the bicyclic monoid, and

\langle a,b \,\vert\; aba=baa, bba=bab\rangle

is the plactic monoid of degree 2 (it has infinite order). Elements of this plactic monoid may be written as 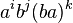$a^ib^j(ba)^k$ for integers i, j, k, as the relations show that ba commutes with both a and b.

Inverse monoids and semigroups

Presentations of inverse monoids and semigroups can be defined in a similar way using a pair

(X;T)

where

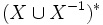
$(X\cup X^{-1})^*$

is the free monoid with involution on $X$ , and

T\subseteq (X\cup X^{-1})^*\times (X\cup X^{-1})^*

is a binary relation between words. We denote by 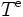$T^{\mathrm{e}}$ (respectively 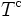$T^\mathrm{c}$ ) the equivalence relation (respectively, the congruence) generated by T.

We use this pair of objects to define an inverse monoid

\mathrm{Inv}^1 \langle X | T\rangle.

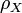Let $\rho_X$ be the Wagner congruence on $X$ , we define the inverse monoid

\mathrm{Inv}^1 \langle X | T\rangle

presented by 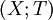$(X;T)$ as

\mathrm{Inv}^1 \langle X | T\rangle=(X\cup X^{-1})^*/(T\cup\rho_X)^{\mathrm{c}}.

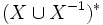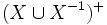In the previous discussion, if we replace everywhere $({X\cup X^{-1}})^*$ with $({X\cup X^{-1}})^+$ we obtain a presentation (for an inverse semigroup) 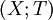$(X;T)$ and an inverse semigroup 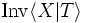$\mathrm{Inv}\langle X | T\rangle$ presented by $(X;T)$ .

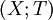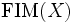A trivial but important example is the free inverse monoid (or free inverse semigroup) on $X$ , that is usually denoted by $\mathrm{FIM}(X)$ (respectively 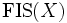$\mathrm{FIS}(X)$ ) and is defined by

\mathrm{FIM}(X)=\mathrm{Inv}^1 \langle X | \varnothing\rangle=({X\cup X^{-1}})^*/\rho_X,

\mathrm{FIS}(X)=\mathrm{Inv} \langle X | \varnothing\rangle=({X\cup X^{-1}})^+/\rho_X.

Notes

↑ Book and Otto, Theorem 7.1.7, p. 149

References

John M. Howie, Fundamentals of Semigroup Theory (1995), Clarendon Press, Oxford ISBN 0-19-851194-9
M. Kilp, U. Knauer, A.V. Mikhalev, Monoids, Acts and Categories with Applications to Wreath Products and Graphs, De Gruyter Expositions in Mathematics vol. 29, Walter de Gruyter, 2000, ISBN 3-11-015248-7.
Ronald V. Book and Friedrich Otto, String-rewriting Systems, Springer, 1993, ISBN 0-387-97965-4, chapter 7, "Algebraic Properties"